A neural network-based approach to hybrid systems identification for control

We consider the problem of designing a machine learning-based model of an unknown dynamical system from a finite number of (state-input)-successor state data points, such that the model obtained is also suitable for optimal control design. We propose a specific neural network (NN) architecture that yields a hybrid system with piecewise-affine dynamics that is differentiable with respect to the network's parameters, thereby enabling the use of derivative-based training procedures. We show that a careful choice of our NN's weights produces a hybrid system model with structural properties that are highly favourable when used as part of a finite horizon optimal control problem (OCP). Specifically, we show that optimal solutions with strong local optimality guarantees can be computed via nonlinear programming, in contrast to classical OCPs for general hybrid systems which typically require mixed-integer optimization. In addition to being well-suited for optimal control design, numerical simulations illustrate that our NN-based technique enjoys very similar performance to state-of-the-art system identification methodologies for hybrid systems and it is competitive on nonlinear benchmarks.

A learning-based approach to multi-agent decision-making

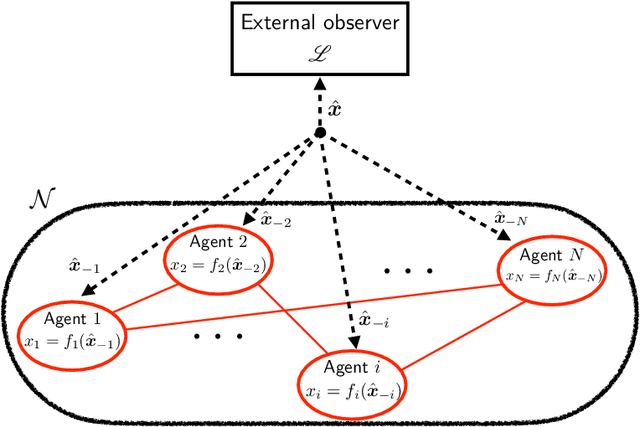
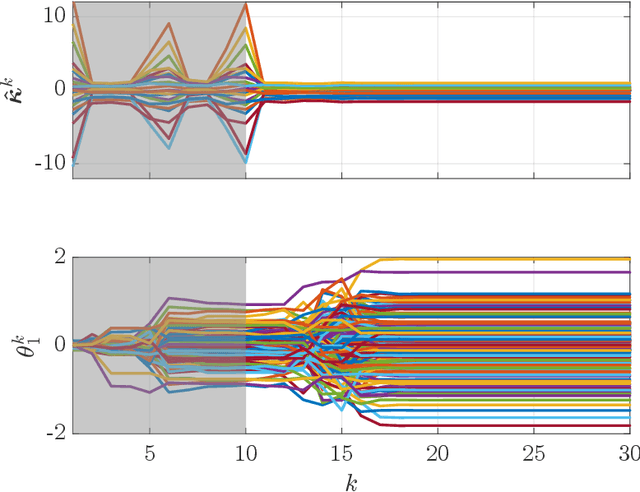
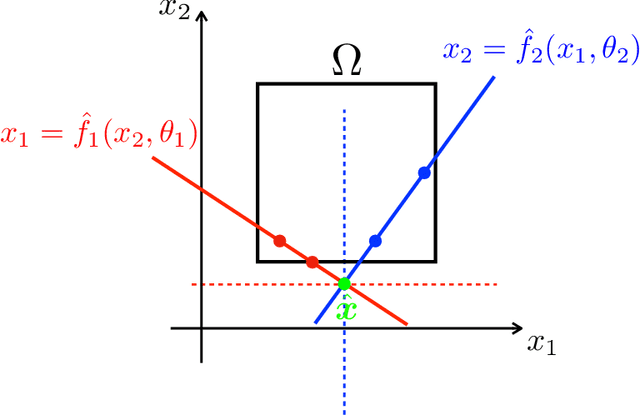
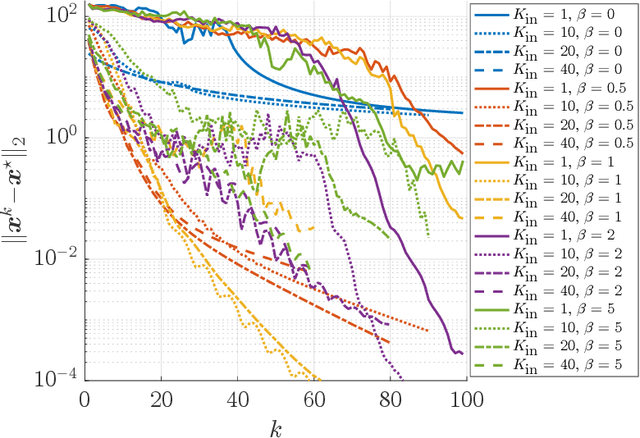
We propose a learning-based methodology to reconstruct private information held by a population of interacting agents in order to predict an exact outcome of the underlying multi-agent interaction process, here identified as a stationary action profile. We envision a scenario where an external observer, endowed with a learning procedure, is allowed to make queries and observe the agents' reactions through private action-reaction mappings, whose collective fixed point corresponds to a stationary profile. By adopting a smart query process to iteratively collect sensible data and update parametric estimates, we establish sufficient conditions to assess the asymptotic properties of the proposed learning-based methodology so that, if convergence happens, it can only be towards a stationary action profile. This fact yields two main consequences: i) learning locally-exact surrogates of the action-reaction mappings allows the external observer to succeed in its prediction task, and ii) working with assumptions so general that a stationary profile is not even guaranteed to exist, the established sufficient conditions hence act also as certificates for the existence of such a desirable profile. Extensive numerical simulations involving typical competitive multi-agent control and decision making problems illustrate the practical effectiveness of the proposed learning-based approach.

Neural network controllers for uncertain linear systems

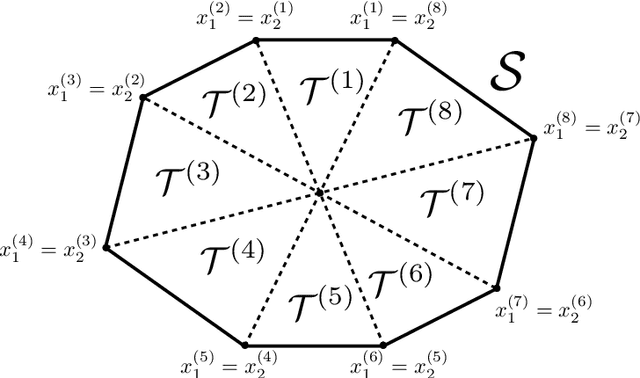
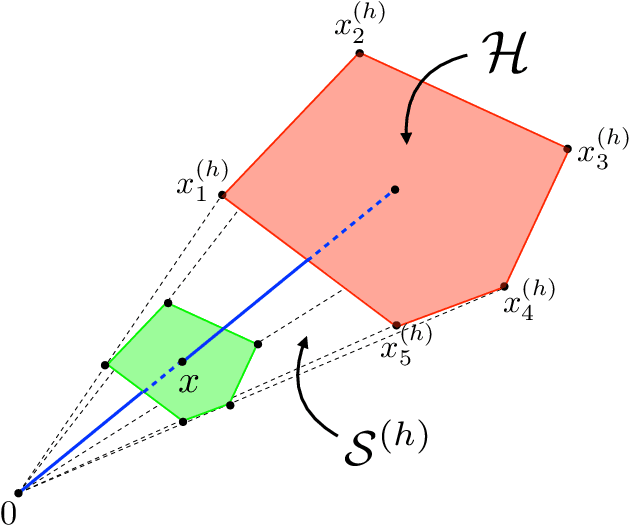
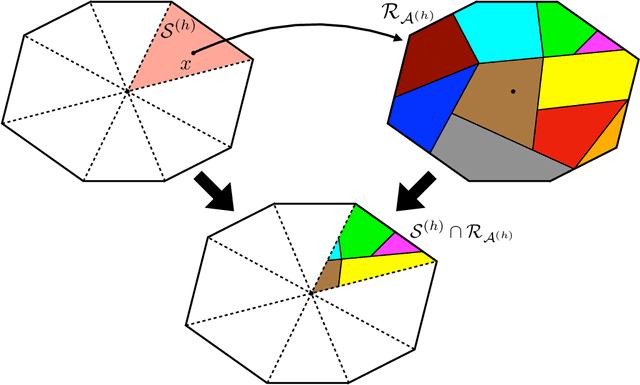
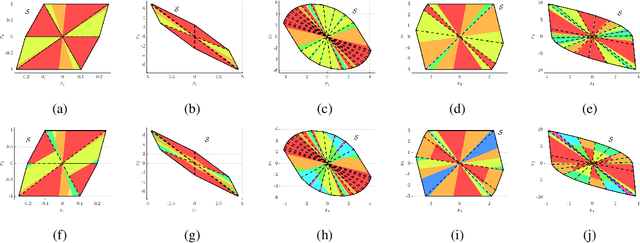
We consider the design of reliable neural network (NN)-based approximations of traditional stabilizing controllers for linear systems affected by polytopic uncertainty, including controllers with variable structure and those based on a minimal selection policy. We develop a systematic procedure to certify the closed-loop stability and performance of a polytopic system when a rectified linear unit (ReLU)-based approximation replaces such traditional controllers. We provide sufficient conditions to ensure stability involving the worst-case approximation error and the Lipschitz constant characterizing the error function between ReLU-based and traditional controller-based state-to-input mappings, and further provide offline, mixed-integer optimization-based methods that allow us to compute those quantities exactly.

Personalized incentives as feedback design in generalized Nash equilibrium problems

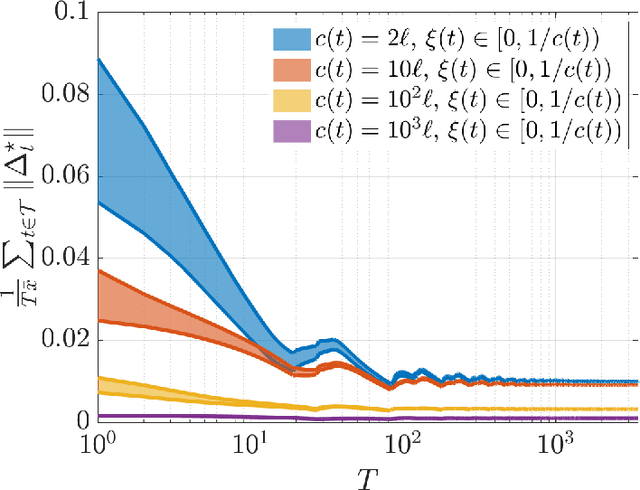
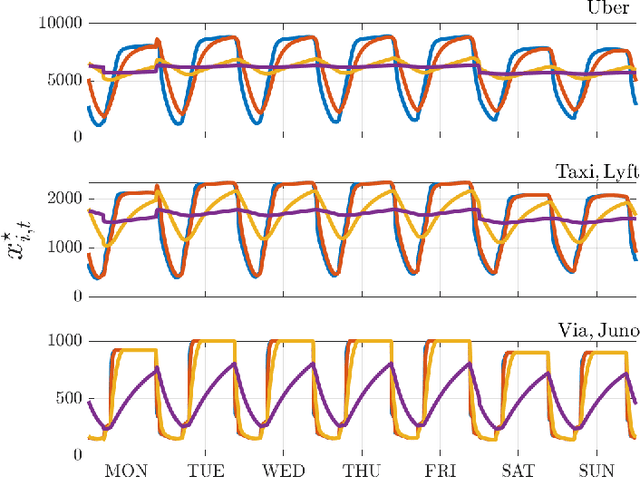
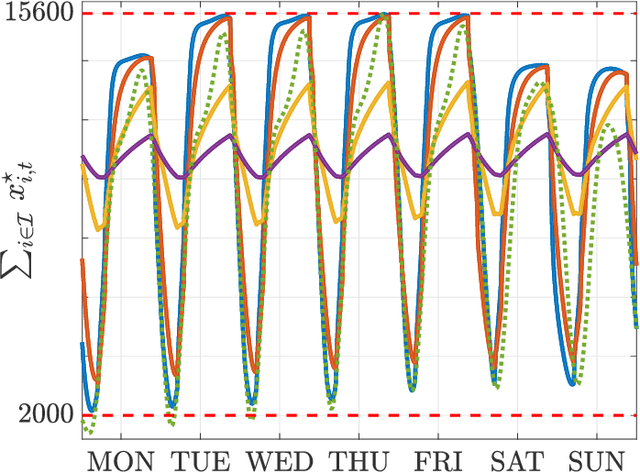
We investigate both stationary and time-varying, nonmonotone generalized Nash equilibrium problems that exhibit symmetric interactions among the agents, which are known to be potential. As may happen in practical cases, however, we envision a scenario in which the formal expression of the underlying potential function is not available, and we design a semi-decentralized Nash equilibrium seeking algorithm. In the proposed two-layer scheme, a coordinator iteratively integrates the (possibly noisy and sporadic) agents' feedback to learn the pseudo-gradients of the agents, and then design personalized incentives for them. On their side, the agents receive those personalized incentives, compute a solution to an extended game, and then return feedback measurements to the coordinator. In the stationary setting, our algorithm returns a Nash equilibrium in case the coordinator is endowed with standard learning policies, while it returns a Nash equilibrium up to a constant, yet adjustable, error in the time-varying case. As a motivating application, we consider the ridehailing service provided by several companies with mobility as a service orchestration, necessary to both handle competition among firms and avoid traffic congestion, which is also adopted to run numerical experiments verifying our results.

Reliably-stabilizing piecewise-affine neural network controllers

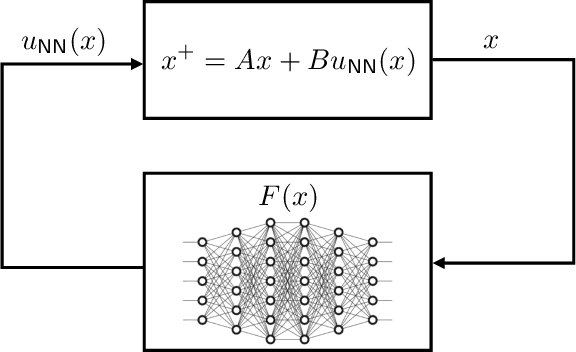
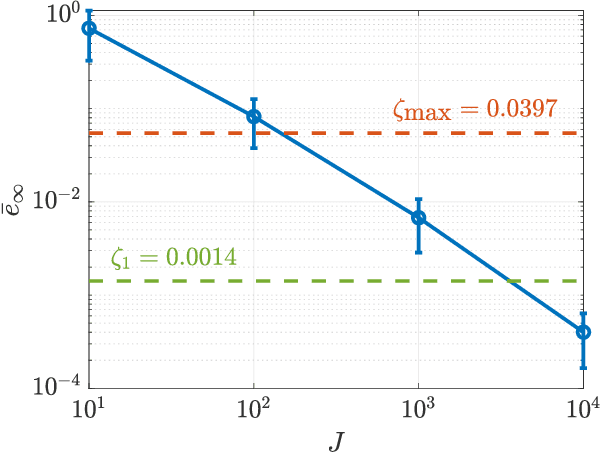
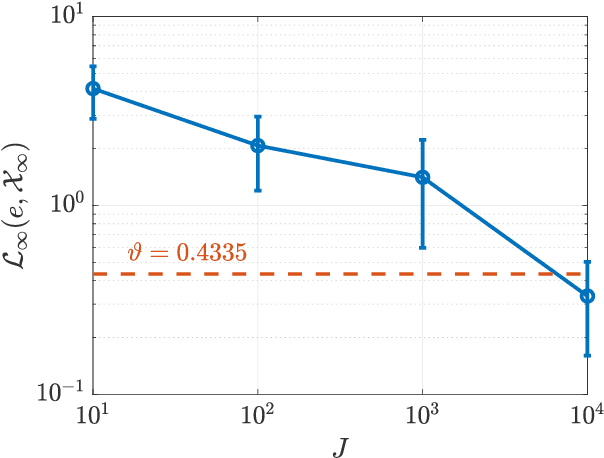
A common problem affecting neural network (NN) approximations of model predictive control (MPC) policies is the lack of analytical tools to assess the stability of the closed-loop system under the action of the NN-based controller. We present a general procedure to quantify the performance of such a controller, or to design minimum complexity NNs with rectified linear units (ReLUs) that preserve the desirable properties of a given MPC scheme. By quantifying the approximation error between NN-based and MPC-based state-to-input mappings, we first establish suitable conditions involving two key quantities, the worst-case error and the Lipschitz constant, guaranteeing the stability of the closed-loop system. We then develop an offline, mixed-integer optimization-based method to compute those quantities exactly. Together these techniques provide conditions sufficient to certify the stability and performance of a ReLU-based approximation of an MPC control law.

Learning equilibria with personalized incentives in a class of nonmonotone games

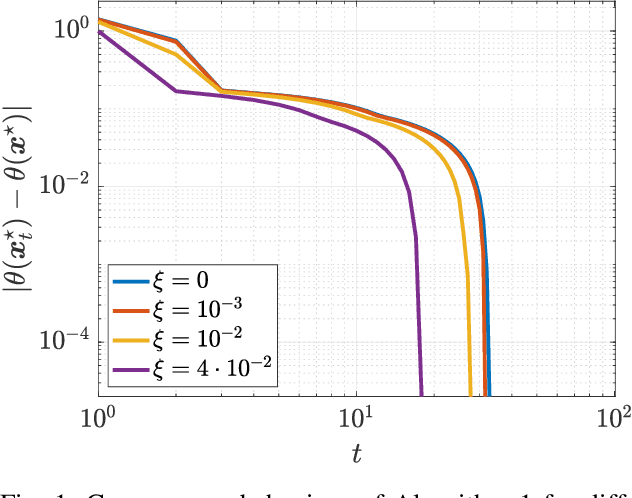
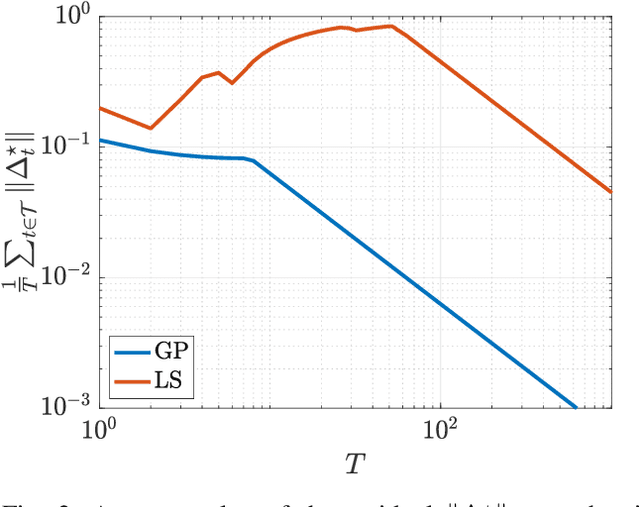
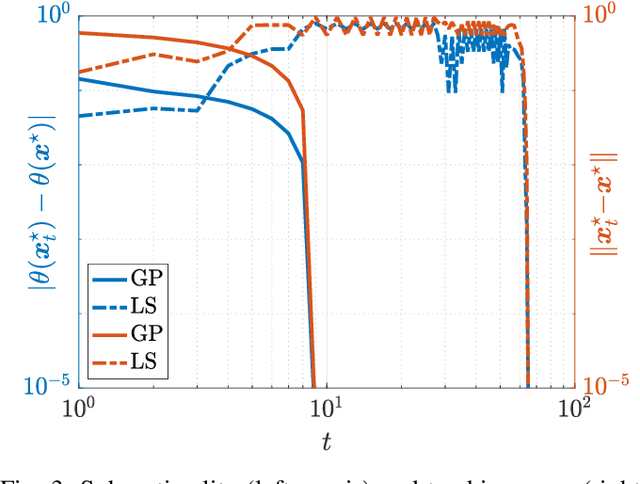
We consider quadratic, nonmonotone generalized Nash equilibrium problems with symmetric interactions among the agents, which are known to be potential. As may happen in practical cases, we envision a scenario in which an explicit expression of the underlying potential function is not available, and we design a two-layer Nash equilibrium seeking algorithm. In the proposed scheme, a coordinator iteratively integrates the noisy agents' feedback to learn the pseudo-gradients of the agents, and then design personalized incentives for them. On their side, the agents receive those personalized incentives, compute a solution to an extended game, and then return feedback measures to the coordinator. We show that our algorithm returns an equilibrium in case the coordinator is endowed with standard learning policies, and corroborate our results on a numerical instance of a hypomonotone game.

An optimal transport approach to data compression in distributionally robust control

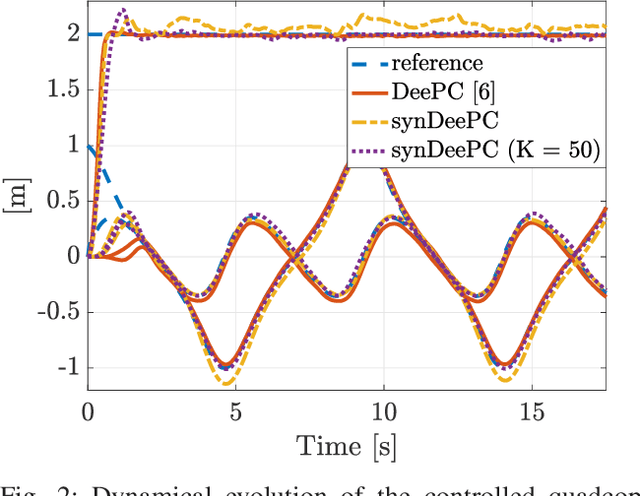
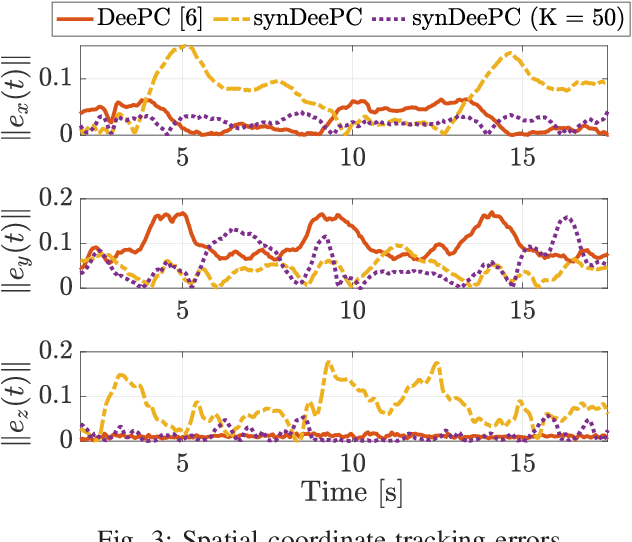
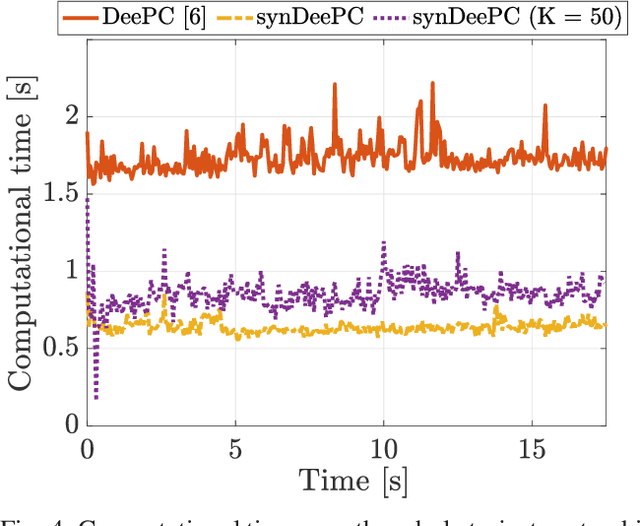
We consider the problem of controlling a stochastic linear time-invariant system using a behavioural approach based on the direct optimization of controllers over input-output pairs drawn from a large dataset. In order to improve the computational efficiency of controllers implemented online, we propose a method for compressing this large data set to a smaller synthetic set of representative behaviours using techniques based on optimal transport. Specifically, we choose our synthetic data by minimizing the Wasserstein distance between atomic distributions supported on both the original data set and our synthetic one. We show that a distributionally robust optimal control computed using our synthetic dataset enjoys the same performance guarantees onto an arbitrarily larger ambiguity set relative to the original one. Finally, we illustrate the robustness and control performances over the original and compressed datasets through numerical simulations.