Learning Algorithm Hyperparameters for Fast Parametric Convex Optimization

We introduce a machine-learning framework to learn the hyperparameter sequence of first-order methods (e.g., the step sizes in gradient descent) to quickly solve parametric convex optimization problems. Our computational architecture amounts to running fixed-point iterations where the hyperparameters are the same across all parametric instances and consists of two phases. In the first step-varying phase the hyperparameters vary across iterations, while in the second steady-state phase the hyperparameters are constant across iterations. Our learned optimizer is flexible in that it can be evaluated on any number of iterations and is guaranteed to converge to an optimal solution. To train, we minimize the mean square error to a ground truth solution. In the case of gradient descent, the one-step optimal step size is the solution to a least squares problem, and in the case of unconstrained quadratic minimization, we can compute the two and three-step optimal solutions in closed-form. In other cases, we backpropagate through the algorithm steps to minimize the training objective after a given number of steps. We show how to learn hyperparameters for several popular algorithms: gradient descent, proximal gradient descent, and two ADMM-based solvers: OSQP and SCS. We use a sample convergence bound to obtain generalization guarantees for the performance of our learned algorithm for unseen data, providing both lower and upper bounds. We showcase the effectiveness of our method with many examples, including ones from control, signal processing, and machine learning. Remarkably, our approach is highly data-efficient in that we only use $10$ problem instances to train the hyperparameters in all of our examples.

Data-Driven Performance Guarantees for Classical and Learned Optimizers

We introduce a data-driven approach to analyze the performance of continuous optimization algorithms using generalization guarantees from statistical learning theory. We study classical and learned optimizers to solve families of parametric optimization problems. We build generalization guarantees for classical optimizers, using a sample convergence bound, and for learned optimizers, using the Probably Approximately Correct (PAC)-Bayes framework. To train learned optimizers, we use a gradient-based algorithm to directly minimize the PAC-Bayes upper bound. Numerical experiments in signal processing, control, and meta-learning showcase the ability of our framework to provide strong generalization guarantees for both classical and learned optimizers given a fixed budget of iterations. For classical optimizers, our bounds are much tighter than those that worst-case guarantees provide. For learned optimizers, our bounds outperform the empirical outcomes observed in their non-learned counterparts.

A neural network-based approach to hybrid systems identification for control

We consider the problem of designing a machine learning-based model of an unknown dynamical system from a finite number of (state-input)-successor state data points, such that the model obtained is also suitable for optimal control design. We propose a specific neural network (NN) architecture that yields a hybrid system with piecewise-affine dynamics that is differentiable with respect to the network's parameters, thereby enabling the use of derivative-based training procedures. We show that a careful choice of our NN's weights produces a hybrid system model with structural properties that are highly favourable when used as part of a finite horizon optimal control problem (OCP). Specifically, we show that optimal solutions with strong local optimality guarantees can be computed via nonlinear programming, in contrast to classical OCPs for general hybrid systems which typically require mixed-integer optimization. In addition to being well-suited for optimal control design, numerical simulations illustrate that our NN-based technique enjoys very similar performance to state-of-the-art system identification methodologies for hybrid systems and it is competitive on nonlinear benchmarks.

Learning Hierarchical Control For Multi-Agent Capacity-Constrained Systems

This paper introduces a novel data-driven hierarchical control scheme for managing a fleet of nonlinear, capacity-constrained autonomous agents in an iterative environment. We propose a control framework consisting of a high-level dynamic task assignment and routing layer and low-level motion planning and tracking layer. Each layer of the control hierarchy uses a data-driven Model Predictive Control (MPC) policy, maintaining bounded computational complexity at each calculation of a new task assignment or actuation input. We utilize collected data to iteratively refine estimates of agent capacity usage, and update MPC policy parameters accordingly. Our approach leverages tools from iterative learning control to integrate learning at both levels of the hierarchy, and coordinates learning between levels in order to maintain closed-loop feasibility and performance improvement of the connected architecture.

Who Plays First? Optimizing the Order of Play in Stackelberg Games with Many Robots

We consider the multi-agent spatial navigation problem of computing the socially optimal order of play, i.e., the sequence in which the agents commit to their decisions, and its associated equilibrium in an N-player Stackelberg trajectory game. We model this problem as a mixed-integer optimization problem over the space of all possible Stackelberg games associated with the order of play's permutations. To solve the problem, we introduce Branch and Play (B&P), an efficient and exact algorithm that provably converges to a socially optimal order of play and its Stackelberg equilibrium. As a subroutine for B&P, we employ and extend sequential trajectory planning, i.e., a popular multi-agent control approach, to scalably compute valid local Stackelberg equilibria for any given order of play. We demonstrate the practical utility of B&P to coordinate air traffic control, swarm formation, and delivery vehicle fleets. We find that B&P consistently outperforms various baselines, and computes the socially optimal equilibrium.

Differentiable Cutting-plane Layers for Mixed-integer Linear Optimization

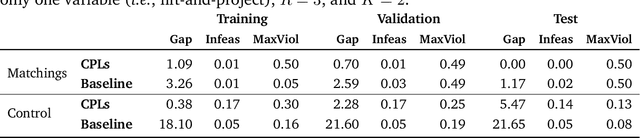
We consider the problem of solving a family of parametric mixed-integer linear optimization problems where some entries in the input data change. We introduce the concept of cutting-plane layer (CPL), i.e., a differentiable cutting-plane generator mapping the problem data and previous iterates to cutting planes. We propose a CPL implementation to generate split cuts, and by combining several CPLs, we devise a differentiable cutting-plane algorithm that exploits the repeated nature of parametric instances. In an offline phase, we train our algorithm by updating the internal parameters controlling the CPLs, thus altering cut generation. Once trained, our algorithm computes, with predictable execution times and a fixed number of cuts, solutions with low integrality gaps. Preliminary computational tests show that our algorithm generalizes on unseen instances and captures underlying parametric structures.

Learning to Warm-Start Fixed-Point Optimization Algorithms

We introduce a machine-learning framework to warm-start fixed-point optimization algorithms. Our architecture consists of a neural network mapping problem parameters to warm starts, followed by a predefined number of fixed-point iterations. We propose two loss functions designed to either minimize the fixed-point residual or the distance to a ground truth solution. In this way, the neural network predicts warm starts with the end-to-end goal of minimizing the downstream loss. An important feature of our architecture is its flexibility, in that it can predict a warm start for fixed-point algorithms run for any number of steps, without being limited to the number of steps it has been trained on. We provide PAC-Bayes generalization bounds on unseen data for common classes of fixed-point operators: contractive, linearly convergent, and averaged. Applying this framework to well-known applications in control, statistics, and signal processing, we observe a significant reduction in the number of iterations and solution time required to solve these problems, through learned warm starts.

Is Bang-Bang Control All You Need? Solving Continuous Control with Bernoulli Policies

Reinforcement learning (RL) for continuous control typically employs distributions whose support covers the entire action space. In this work, we investigate the colloquially known phenomenon that trained agents often prefer actions at the boundaries of that space. We draw theoretical connections to the emergence of bang-bang behavior in optimal control, and provide extensive empirical evaluation across a variety of recent RL algorithms. We replace the normal Gaussian by a Bernoulli distribution that solely considers the extremes along each action dimension - a bang-bang controller. Surprisingly, this achieves state-of-the-art performance on several continuous control benchmarks - in contrast to robotic hardware, where energy and maintenance cost affect controller choices. Since exploration, learning,and the final solution are entangled in RL, we provide additional imitation learning experiments to reduce the impact of exploration on our analysis. Finally, we show that our observations generalize to environments that aim to model real-world challenges and evaluate factors to mitigate the emergence of bang-bang solutions. Our findings emphasize challenges for benchmarking continuous control algorithms, particularly in light of potential real-world applications.

Accelerating Quadratic Optimization with Reinforcement Learning

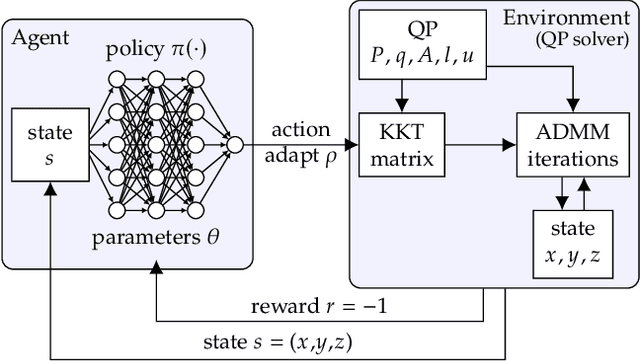
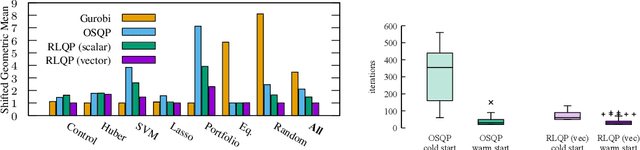
First-order methods for quadratic optimization such as OSQP are widely used for large-scale machine learning and embedded optimal control, where many related problems must be rapidly solved. These methods face two persistent challenges: manual hyperparameter tuning and convergence time to high-accuracy solutions. To address these, we explore how Reinforcement Learning (RL) can learn a policy to tune parameters to accelerate convergence. In experiments with well-known QP benchmarks we find that our RL policy, RLQP, significantly outperforms state-of-the-art QP solvers by up to 3x. RLQP generalizes surprisingly well to previously unseen problems with varying dimension and structure from different applications, including the QPLIB, Netlib LP and Maros-Meszaros problems. Code for RLQP is available at https://github.com/berkeleyautomation/rlqp.

From predictions to prescriptions: A data-driven response to COVID-19

The COVID-19 pandemic has created unprecedented challenges worldwide. Strained healthcare providers make difficult decisions on patient triage, treatment and care management on a daily basis. Policy makers have imposed social distancing measures to slow the disease, at a steep economic price. We design analytical tools to support these decisions and combat the pandemic. Specifically, we propose a comprehensive data-driven approach to understand the clinical characteristics of COVID-19, predict its mortality, forecast its evolution, and ultimately alleviate its impact. By leveraging cohort-level clinical data, patient-level hospital data, and census-level epidemiological data, we develop an integrated four-step approach, combining descriptive, predictive and prescriptive analytics. First, we aggregate hundreds of clinical studies into the most comprehensive database on COVID-19 to paint a new macroscopic picture of the disease. Second, we build personalized calculators to predict the risk of infection and mortality as a function of demographics, symptoms, comorbidities, and lab values. Third, we develop a novel epidemiological model to project the pandemic's spread and inform social distancing policies. Fourth, we propose an optimization model to re-allocate ventilators and alleviate shortages. Our results have been used at the clinical level by several hospitals to triage patients, guide care management, plan ICU capacity, and re-distribute ventilators. At the policy level, they are currently supporting safe back-to-work policies at a major institution and equitable vaccine distribution planning at a major pharmaceutical company, and have been integrated into the US Center for Disease Control's pandemic forecast.