Who Plays First? Optimizing the Order of Play in Stackelberg Games with Many Robots

We consider the multi-agent spatial navigation problem of computing the socially optimal order of play, i.e., the sequence in which the agents commit to their decisions, and its associated equilibrium in an N-player Stackelberg trajectory game. We model this problem as a mixed-integer optimization problem over the space of all possible Stackelberg games associated with the order of play's permutations. To solve the problem, we introduce Branch and Play (B&P), an efficient and exact algorithm that provably converges to a socially optimal order of play and its Stackelberg equilibrium. As a subroutine for B&P, we employ and extend sequential trajectory planning, i.e., a popular multi-agent control approach, to scalably compute valid local Stackelberg equilibria for any given order of play. We demonstrate the practical utility of B&P to coordinate air traffic control, swarm formation, and delivery vehicle fleets. We find that B&P consistently outperforms various baselines, and computes the socially optimal equilibrium.

Differentiable Cutting-plane Layers for Mixed-integer Linear Optimization

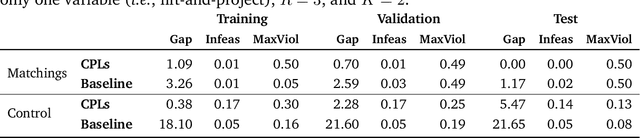
We consider the problem of solving a family of parametric mixed-integer linear optimization problems where some entries in the input data change. We introduce the concept of cutting-plane layer (CPL), i.e., a differentiable cutting-plane generator mapping the problem data and previous iterates to cutting planes. We propose a CPL implementation to generate split cuts, and by combining several CPLs, we devise a differentiable cutting-plane algorithm that exploits the repeated nature of parametric instances. In an offline phase, we train our algorithm by updating the internal parameters controlling the CPLs, thus altering cut generation. Once trained, our algorithm computes, with predictable execution times and a fixed number of cuts, solutions with low integrality gaps. Preliminary computational tests show that our algorithm generalizes on unseen instances and captures underlying parametric structures.