Learning Hierarchical Control For Multi-Agent Capacity-Constrained Systems

This paper introduces a novel data-driven hierarchical control scheme for managing a fleet of nonlinear, capacity-constrained autonomous agents in an iterative environment. We propose a control framework consisting of a high-level dynamic task assignment and routing layer and low-level motion planning and tracking layer. Each layer of the control hierarchy uses a data-driven Model Predictive Control (MPC) policy, maintaining bounded computational complexity at each calculation of a new task assignment or actuation input. We utilize collected data to iteratively refine estimates of agent capacity usage, and update MPC policy parameters accordingly. Our approach leverages tools from iterative learning control to integrate learning at both levels of the hierarchy, and coordinates learning between levels in order to maintain closed-loop feasibility and performance improvement of the connected architecture.

Data-Driven Strategies for Hierarchical Predictive Control in Unknown Environments

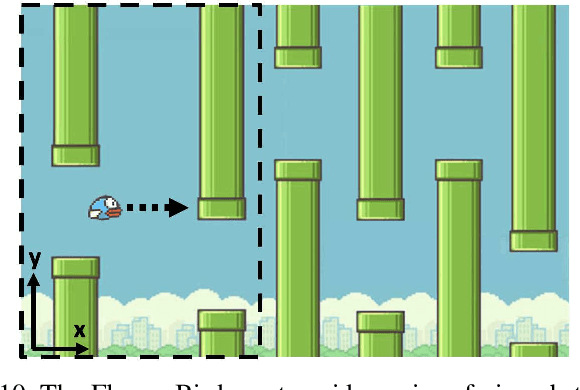
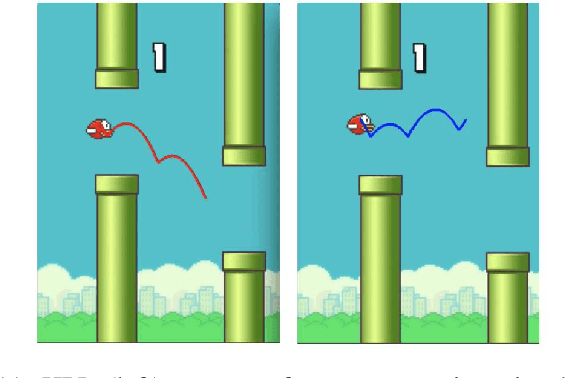
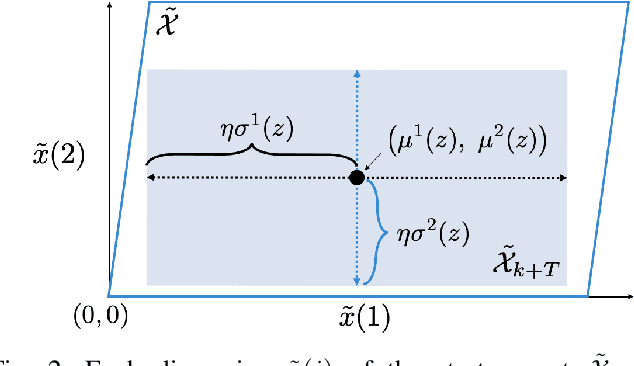
This article proposes a hierarchical learning architecture for safe data-driven control in unknown environments. We consider a constrained nonlinear dynamical system and assume the availability of state-input trajectories solving control tasks in different environments. In addition to task-invariant system state and input constraints, a parameterized environment model generates task-specific state constraints, which are satisfied by the stored trajectories. Our goal is to use these trajectories to find a safe and high-performing policy for a new task in a new, unknown environment. We propose using the stored data to learn generalizable control strategies. At each time step, based on a local forecast of the new task environment, the learned strategy consists of a target region in the state space and input constraints to guide the system evolution to the target region. These target regions are used as terminal sets by a low-level model predictive controller. We show how to i) design the target sets from past data and then ii) incorporate them into a model predictive control scheme with shifting horizon that ensures safety of the closed-loop system when performing the new task. We prove the feasibility of the resulting control policy, and apply the proposed method to robotic path planning, racing, and computer game applications.

Learning to Satisfy Unknown Constraints in Iterative MPC

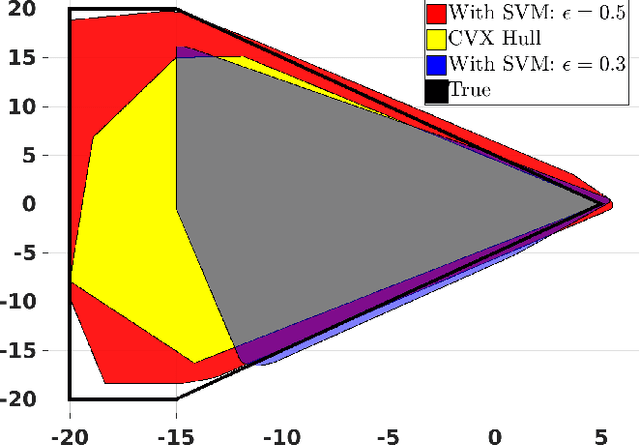
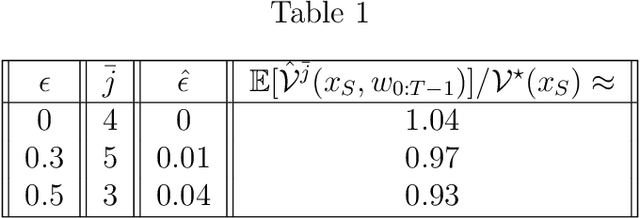
We propose a control design method for linear time-invariant systems that iteratively learns to satisfy unknown polyhedral state constraints. At each iteration of a repetitive task, the method constructs an estimate of the unknown environment constraints using collected closed-loop trajectory data. This estimated constraint set is improved iteratively upon collection of additional data. An MPC controller is then designed to robustly satisfy the estimated constraint set. This paper presents the details of the proposed approach, and provides robust and probabilistic guarantees of constraint satisfaction as a function of the number of executed task iterations. We demonstrate the efficacy of the proposed framework in a detailed numerical example.

Exploiting Model Sparsity in Adaptive MPC: A Compressed Sensing Viewpoint

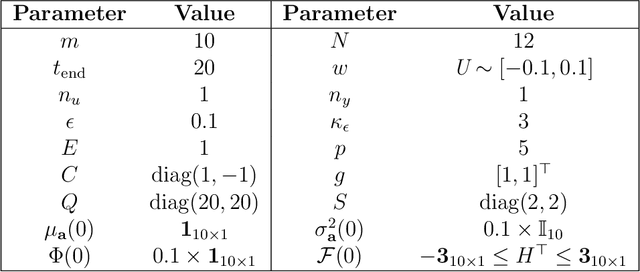
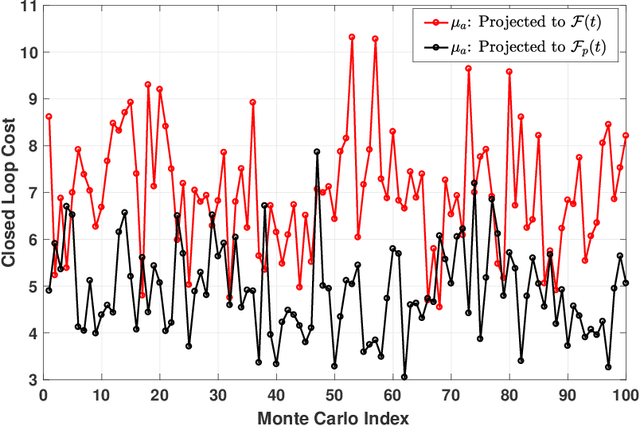
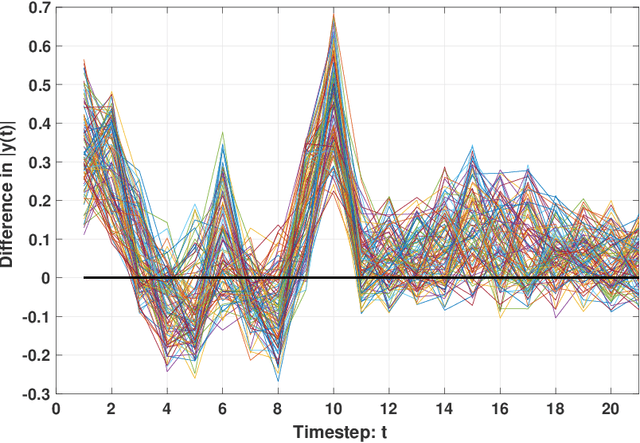
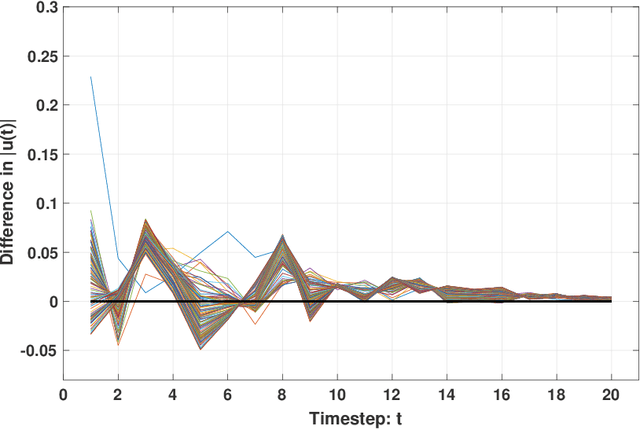
This paper proposes an Adaptive Stochastic Model Predictive Control (MPC) strategy for stable linear time-invariant systems in the presence of bounded disturbances. We consider multi-input, multi-output systems that can be expressed by a Finite Impulse Response (FIR) model. The parameters of the FIR model corresponding to each output are unknown but assumed sparse. We estimate these parameters using the Recursive Least Squares algorithm. The estimates are then improved using set-based bounds obtained by solving the Basis Pursuit Denoising [1] problem. Our approach is able to handle hard input constraints and probabilistic output constraints. Using tools from distributionally robust optimization, we reformulate the probabilistic output constraints as tractable convex second-order cone constraints, which enables us to pose our MPC design task as a convex optimization problem. The efficacy of the developed algorithm is highlighted with a thorough numerical example, where we demonstrate performance gain over the counterpart algorithm of [2], which does not utilize the sparsity information of the system impulse response parameters during control design.

Model-Based Task Transfer Learning

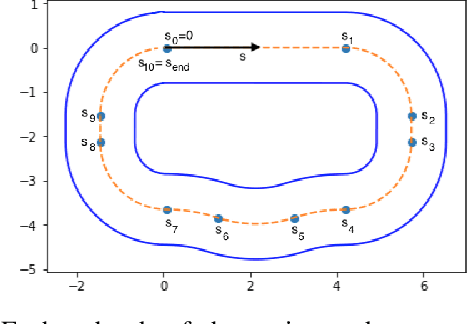
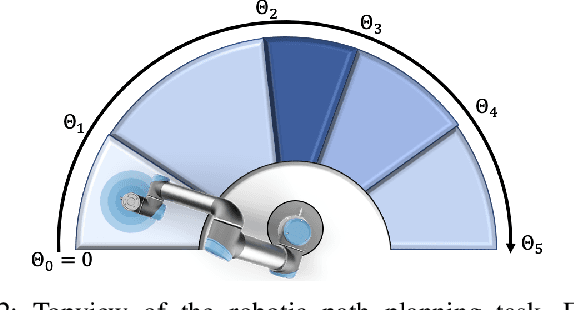
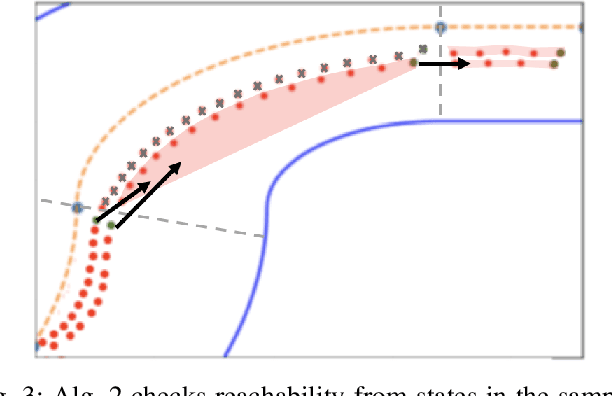
A model-based task transfer learning (MBTTL) method is presented. We consider a constrained nonlinear dynamical system and assume that a dataset of state and input pairs that solve a task T1 is available. Our objective is to find a feasible state-feedback policy for a second task, T1, by using stored data from T2. Our approach applies to tasks T2 which are composed of the same subtasks as T1, but in different order. In this paper we formally introduce the definition of subtask, the MBTTL problem and provide examples of MBTTL in the fields of autonomous cars and manipulators. Then, a computationally efficient approach to solve the MBTTL problem is presented along with proofs of feasibility for constrained linear dynamical systems. Simulation results show the effectiveness of the proposed method.