Learning to Satisfy Unknown Constraints in Iterative MPC

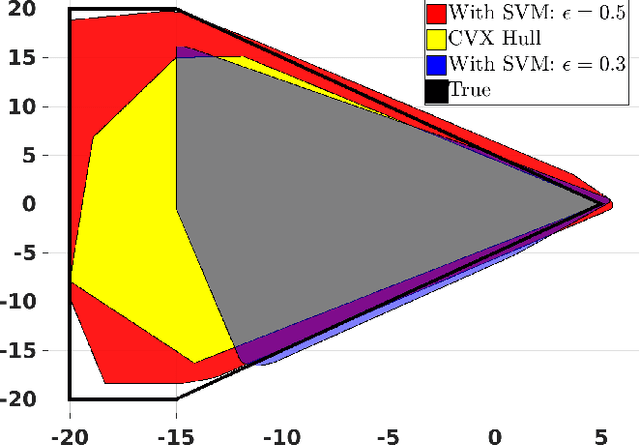
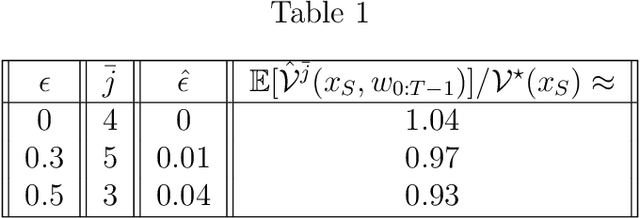
We propose a control design method for linear time-invariant systems that iteratively learns to satisfy unknown polyhedral state constraints. At each iteration of a repetitive task, the method constructs an estimate of the unknown environment constraints using collected closed-loop trajectory data. This estimated constraint set is improved iteratively upon collection of additional data. An MPC controller is then designed to robustly satisfy the estimated constraint set. This paper presents the details of the proposed approach, and provides robust and probabilistic guarantees of constraint satisfaction as a function of the number of executed task iterations. We demonstrate the efficacy of the proposed framework in a detailed numerical example.