Constrained Policy Optimization via Sampling-Based Weight-Space Projection

Safety-critical learning requires policies that improve performance without leaving the safe operating regime. We study constrained policy learning where model parameters must satisfy unknown, rollout-based safety constraints. We propose SCPO, a sampling-based weight-space projection method that enforces safety directly in parameter space without requiring gradient access to the constraint functions. Our approach constructs a local safe region by combining trajectory rollouts with smoothness bounds that relate parameter changes to shifts in safety metrics. Each gradient update is then projected via a convex SOCP, producing a safe first-order step. We establish a safe-by-induction guarantee: starting from any safe initialization, all intermediate policies remain safe given feasible projections. In constrained control settings with a stabilizing backup policy, our approach further ensures closed-loop stability and enables safe adaptation beyond the conservative backup. On regression with harmful supervision and a constrained double-integrator task with malicious expert, our approach consistently rejects unsafe updates, maintains feasibility throughout training, and achieves meaningful primal objective improvement.

Non Normalized Shared-Constraint Dynamic Games for Human-Robot Collaboration with Asymmetric Responsibility

This paper proposes a dynamic game formulation for cooperative human-robot navigation in shared workspaces with obstacles, where the human and robot jointly satisfy shared safety constraints while pursuing a common task. A key contribution is the introduction of a non-normalized equilibrium structure for the shared constraints. This structure allows the two agents to contribute different levels of effort towards enforcing safety requirements such as collision avoidance and inter-players spacing. We embed this non-normalized equilibrium into a receding-horizon optimal control scheme.

Energy-Aware Lane Planning for Connected Electric Vehicles in Urban Traffic: Design and Vehicle-in-the-Loop Validation

Urban driving with connected and automated vehicles (CAVs) offers potential for energy savings, yet most eco-driving strategies focus solely on longitudinal speed control within a single lane. This neglects the significant impact of lateral decisions, such as lane changes, on overall energy efficiency, especially in environments with traffic signals and heterogeneous traffic flow. To address this gap, we propose a novel energy-aware motion planning framework that jointly optimizes longitudinal speed and lateral lane-change decisions using vehicle-to-infrastructure (V2I) communication. Our approach estimates long-term energy costs using a graph-based approximation and solves short-horizon optimal control problems under traffic constraints. Using a data-driven energy model calibrated to an actual battery electric vehicle, we demonstrate with vehicle-in-the-loop experiments that our method reduces motion energy consumption by up to 24 percent compared to a human driver, highlighting the potential of connectivity-enabled planning for sustainable urban autonomy.

Non-Normalized Solutions of Generalized Nash Equilibrium in Autonomous Racing

In dynamic games with shared constraints, Generalized Nash Equilibria (GNE) are often computed using the normalized solution concept, which assumes identical Lagrange multipliers for shared constraints across all players. While widely used, this approach excludes other potentially valuable GNE. This paper addresses the limitations of normalized solutions in racing scenarios through three key contributions. First, we highlight the shortcomings of normalized solutions with a simple racing example. Second, we propose a novel method based on the Mixed Complementarity Problem (MCP) formulation to compute non-normalized Generalized Nash Equilibria (GNE). Third, we demonstrate that our proposed method overcomes the limitations of normalized GNE solutions and enables richer multi-modal interactions in realistic racing scenarios.

A Simple Approach to Constraint-Aware Imitation Learning with Application to Autonomous Racing

Guaranteeing constraint satisfaction is challenging in imitation learning (IL), particularly in tasks that require operating near a system's handling limits. Traditional IL methods often struggle to enforce constraints, leading to suboptimal performance in high-precision tasks. In this paper, we present a simple approach to incorporating safety into the IL objective. Through simulations, we empirically validate our approach on an autonomous racing task with both full-state and image feedback, demonstrating improved constraint satisfaction and greater consistency in task performance compared to a baseline method.

Generalized Nash Equilibrium Solutions in Dynamic Games With Shared Constraints

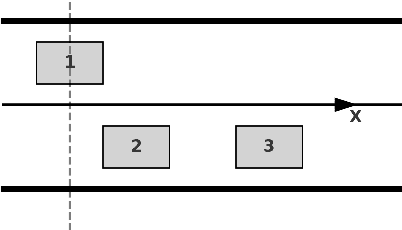
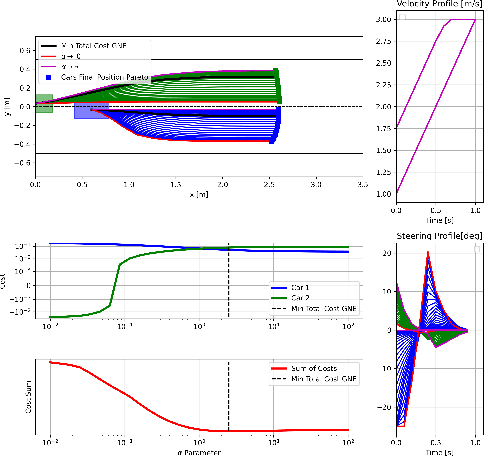
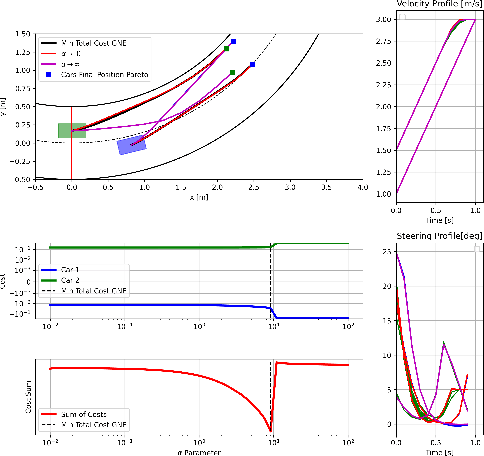
In dynamic games with shared constraints, Generalized Nash Equilibria (GNE) are often computed using the normalized solution concept, which assumes identical Lagrange multipliers for shared constraints across all players. While widely used, this approach excludes other potentially valuable GNE. This paper presents a novel method based on the Mixed Complementarity Problem (MCP) formulation to compute non-normalized GNE, expanding the solution space. We also propose a systematic approach for selecting the optimal GNE based on predefined criteria, enhancing practical flexibility. Numerical examples illustrate the methods effectiveness, offering an alternative to traditional normalized solutions.

Learning Two-agent Motion Planning Strategies from Generalized Nash Equilibrium for Model Predictive Control

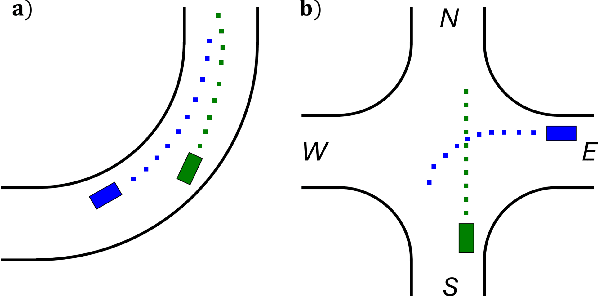
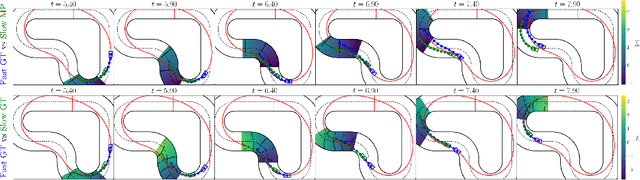
We introduce an Implicit Game-Theoretic MPC (IGT-MPC), a decentralized algorithm for two-agent motion planning that uses a learned value function that predicts the game-theoretic interaction outcomes as the terminal cost-to-go function in a model predictive control (MPC) framework, guiding agents to implicitly account for interactions with other agents and maximize their reward. This approach applies to competitive and cooperative multi-agent motion planning problems which we formulate as constrained dynamic games. Given a constrained dynamic game, we randomly sample initial conditions and solve for the generalized Nash equilibrium (GNE) to generate a dataset of GNE solutions, computing the reward outcome of each game-theoretic interaction from the GNE. The data is used to train a simple neural network to predict the reward outcome, which we use as the terminal cost-to-go function in an MPC scheme. We showcase emerging competitive and coordinated behaviors using IGT-MPC in scenarios such as two-vehicle head-to-head racing and un-signalized intersection navigation. IGT-MPC offers a novel method integrating machine learning and game-theoretic reasoning into model-based decentralized multi-agent motion planning.

A General 3D Road Model for Motorcycle Racing

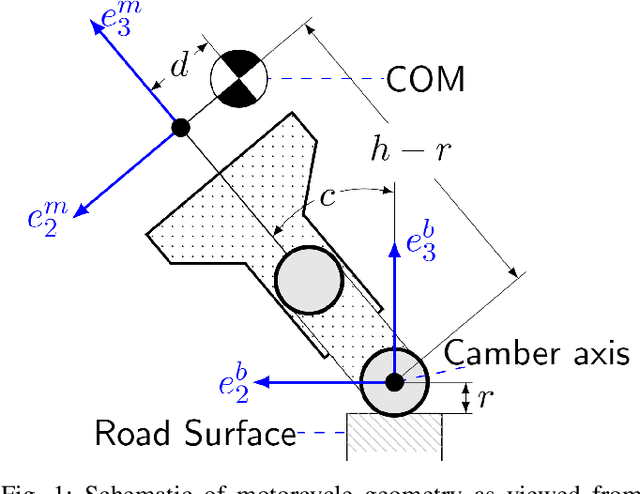
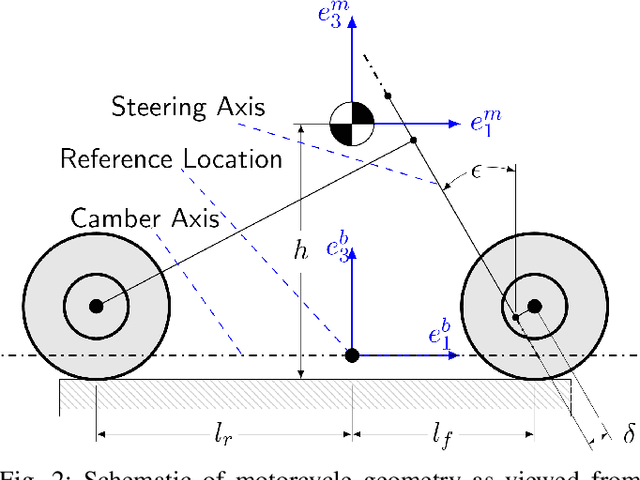
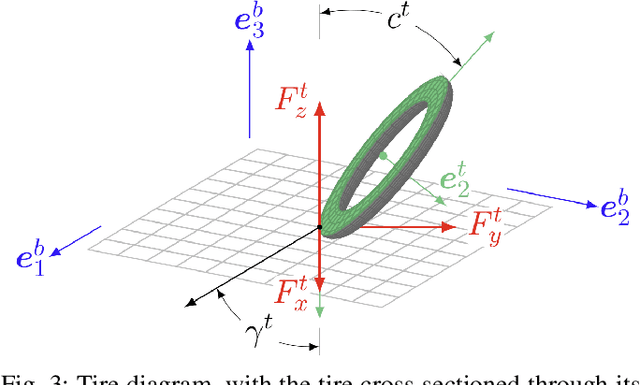
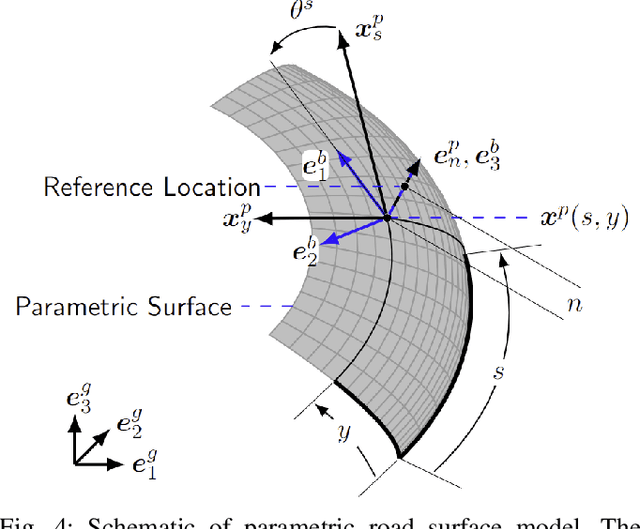
We present a novel control-oriented motorcycle model and use it for computing racing lines on a nonplanar racetrack. The proposed model combines recent advances in nonplanar road models with the dynamics of motorcycles. Our approach considers the additional camber degree of freedom of the motorcycle body with a simplified model of the rider and front steering fork bodies. We demonstrate the effectiveness of our model by computing minimum-time racing trajectories on a nonplanar racetrack.

Predictive Braking on a Nonplanar Road

We present an approach for predictive braking of a four-wheeled vehicle on a nonplanar road. Our main contribution is a methodology to consider friction and road contact safety on general smooth road geometry. We use this to develop an active safety system to preemptively reduce vehicle speed for upcoming road geometry, such as off-camber turns. Our system may be used for human-driven or autonomous vehicles and we demonstrate it with a simulated ADAS scenario. We show that loss of control due to driver error on nonplanar roads can be mitigated by our approach.

A Sequential Quadratic Programming Approach to the Solution of Open-Loop Generalized Nash Equilibria for Autonomous Racing

Dynamic games can be an effective approach for modeling interactive behavior between multiple competitive agents in autonomous racing and they provide a theoretical framework for simultaneous prediction and control in such scenarios. In this work, we propose DG-SQP, a numerical method for the solution of local generalized Nash equilibria (GNE) for open-loop general-sum dynamic games for agents with nonlinear dynamics and constraints. In particular, we formulate a sequential quadratic programming (SQP) approach which requires only the solution of a single convex quadratic program at each iteration. The three key elements of the method are a non-monotonic line search for solving the associated KKT equations, a merit function to handle zero sum costs, and a decaying regularization scheme for SQP step selection. We show that our method achieves linear convergence in the neighborhood of local GNE and demonstrate the effectiveness of the approach in the context of head-to-head car racing, where we show significant improvement in solver success rate when comparing against the state-of-the-art PATH solver for dynamic games. An implementation of our solver can be found at https://github.com/zhu-edward/DGSQP.