Edward L. Zhu
Learning Two-agent Motion Planning Strategies from Generalized Nash Equilibrium for Model Predictive Control
Nov 21, 2024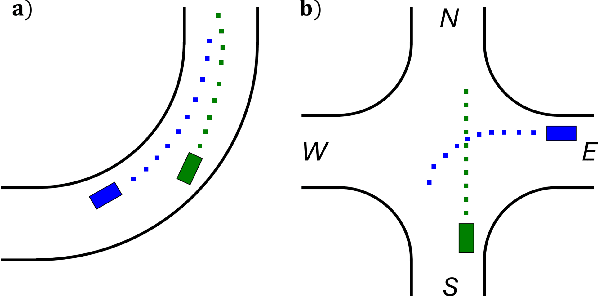


Abstract:We introduce an Implicit Game-Theoretic MPC (IGT-MPC), a decentralized algorithm for two-agent motion planning that uses a learned value function that predicts the game-theoretic interaction outcomes as the terminal cost-to-go function in a model predictive control (MPC) framework, guiding agents to implicitly account for interactions with other agents and maximize their reward. This approach applies to competitive and cooperative multi-agent motion planning problems which we formulate as constrained dynamic games. Given a constrained dynamic game, we randomly sample initial conditions and solve for the generalized Nash equilibrium (GNE) to generate a dataset of GNE solutions, computing the reward outcome of each game-theoretic interaction from the GNE. The data is used to train a simple neural network to predict the reward outcome, which we use as the terminal cost-to-go function in an MPC scheme. We showcase emerging competitive and coordinated behaviors using IGT-MPC in scenarios such as two-vehicle head-to-head racing and un-signalized intersection navigation. IGT-MPC offers a novel method integrating machine learning and game-theoretic reasoning into model-based decentralized multi-agent motion planning.
A Sequential Quadratic Programming Approach to the Solution of Open-Loop Generalized Nash Equilibria for Autonomous Racing
Mar 29, 2024



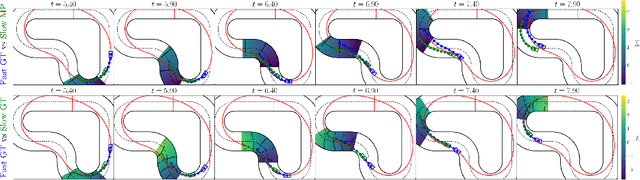
Abstract:Dynamic games can be an effective approach for modeling interactive behavior between multiple competitive agents in autonomous racing and they provide a theoretical framework for simultaneous prediction and control in such scenarios. In this work, we propose DG-SQP, a numerical method for the solution of local generalized Nash equilibria (GNE) for open-loop general-sum dynamic games for agents with nonlinear dynamics and constraints. In particular, we formulate a sequential quadratic programming (SQP) approach which requires only the solution of a single convex quadratic program at each iteration. The three key elements of the method are a non-monotonic line search for solving the associated KKT equations, a merit function to handle zero sum costs, and a decaying regularization scheme for SQP step selection. We show that our method achieves linear convergence in the neighborhood of local GNE and demonstrate the effectiveness of the approach in the context of head-to-head car racing, where we show significant improvement in solver success rate when comparing against the state-of-the-art PATH solver for dynamic games. An implementation of our solver can be found at https://github.com/zhu-edward/DGSQP.
Learning Model Predictive Control with Error Dynamics Regression for Autonomous Racing
Sep 19, 2023Abstract:This work presents a novel Learning Model Predictive Control (LMPC) strategy for autonomous racing at the handling limit that can iteratively explore and learn unknown dynamics in high-speed operational domains. We start from existing LMPC formulations and modify the system dynamics learning method. In particular, our approach uses a nominal, global, nonlinear, physics-based model with a local, linear, data-driven learning of the error dynamics. We conduct experiments in simulation, 1/10th scale hardware, and deployed the proposed LMPC on a full-scale autonomous race car used in the Indy Autonomous Challenge (IAC) with closed loop experiments at the Putnam Park Road Course in Indiana, USA. The results show that the proposed control policy exhibits improved robustness to parameter tuning and data scarcity. Incremental and safety-aware exploration toward the limit of handling and iterative learning of the vehicle dynamics in high-speed domains is observed both in simulations and experiments.
A Gaussian Process Model for Opponent Prediction in Autonomous Racing
Apr 26, 2022



Abstract:In head-to-head racing, performing tightly constrained, but highly rewarding maneuvers, such as overtaking, require an accurate model of interactive behavior of the opposing target vehicle (TV). However, such information is not typically made available in competitive scenarios, we therefore propose to construct a prediction and uncertainty model given data of the TV from previous races. In particular, a one-step Gaussian Process (GP) model is trained on closed-loop interaction data to learn the behavior of a TV driven by an unknown policy. Predictions of the nominal trajectory and associated uncertainty are rolled out via a sampling-based approach and are used in a model predictive control (MPC) policy for the ego vehicle in order to intelligently trade-off between safety and performance when attempting overtaking maneuvers against a TV. We demonstrate the GP-based predictor in closed loop with the MPC policy in simulation races and compare its performance against several predictors from literature. In a Monte Carlo study, we observe that the GP-based predictor achieves similar win rates while maintaining safety in up to 3x more races. We finally demonstrate the prediction and control framework in real-time on hardware experiments.
Collision Avoidance in Tightly-Constrained Environments without Coordination: a Hierarchical Control Approach
Nov 01, 2020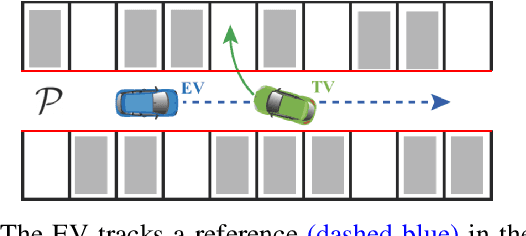
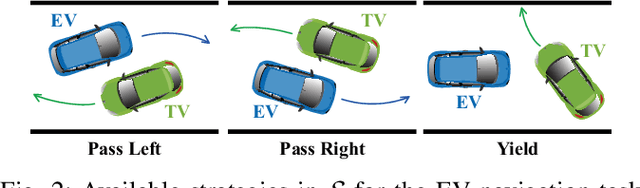


Abstract:We present a hierarchical control approach for maneuvering an autonomous vehicle (AV) in a tightly-constrained environment where other moving AVs and/or human driven vehicles are present. A two-level hierarchy is proposed: a high-level data-driven strategy predictor and a lower-level model-based feedback controller. The strategy predictor maps a high-dimensional environment encoding into a set of high-level strategies. Our approach uses data collected on an offline simulator to train a neural network model as the strategy predictor. Depending on the online selected strategy, a set of time-varying hyperplanes in the AV's motion space is generated and included in the lower level control. The latter is a Strategy-Guided Optimization-Based Collision Avoidance (SG-OBCA) algorithm where the strategy-dependent hyperplane constraints are used to drive a model-based receding horizon controller towards a predicted feasible area. The strategy also informs switching from the SG-OBCA control policy to a safety or emergency control policy. We demonstrate the effectiveness of the proposed data-driven hierarchical control framework in simulations and experiments on a 1/10 scale autonomous car platform where the strategy-guided approach outperforms a model predictive control baseline in both cases.
Trajectory Optimization for Nonlinear Multi-Agent Systems using Decentralized Learning Model Predictive Control
Apr 02, 2020


Abstract:We present a decentralized trajectory optimization scheme based on learning model predictive control for multi-agent systems with nonlinear decoupled dynamics under separable cost and coupled state constraints. By performing the same task iteratively, data from previous task executions is used to construct and improve local time-varying safe sets and an approximate value function. These are used in a decentralized MPC problem as the terminal sets and terminal cost function. Our framework results in a decentralized controller, which requires no communication between agents over each iteration of task execution, and guarantees persistent feasibility, closed-loop stability, and non-decreasing performance of the global system over task iterations. Numerical experiments of a multi-vehicle collision avoidance scenario demonstrate the effectiveness of the proposed scheme.
Inclined Surface Locomotion Strategies for Spherical Tensegrity Robots
Aug 27, 2017
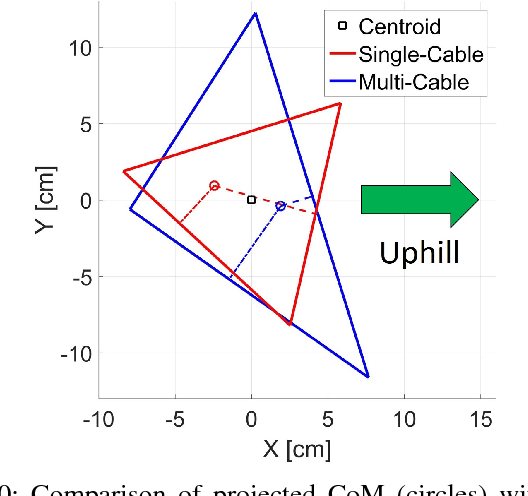
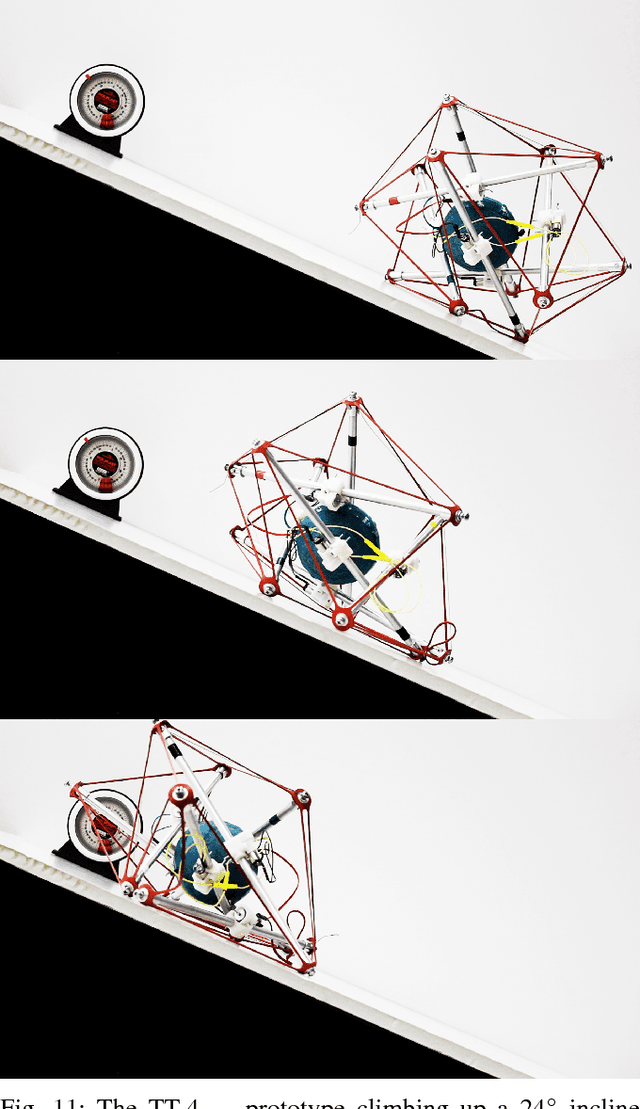
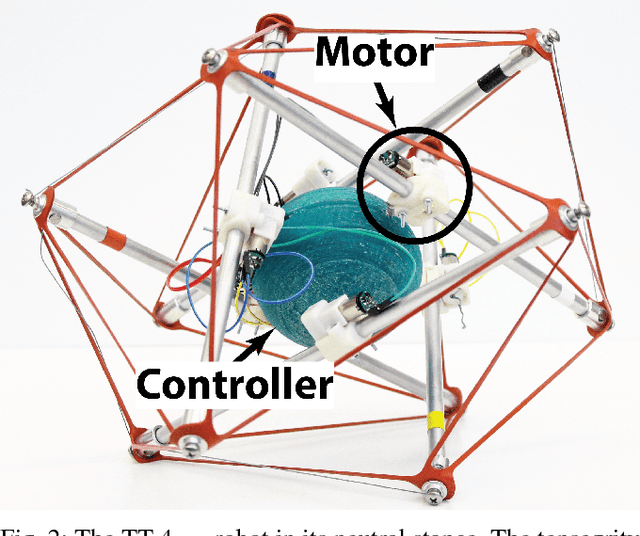
Abstract:This paper presents a new teleoperated spherical tensegrity robot capable of performing locomotion on steep inclined surfaces. With a novel control scheme centered around the simultaneous actuation of multiple cables, the robot demonstrates robust climbing on inclined surfaces in hardware experiments and speeds significantly faster than previous spherical tensegrity models. This robot is an improvement over other iterations in the TT-series and the first tensegrity to achieve reliable locomotion on inclined surfaces of up to 24\degree. We analyze locomotion in simulation and hardware under single and multi-cable actuation, and introduce two novel multi-cable actuation policies, suited for steep incline climbing and speed, respectively. We propose compelling justifications for the increased dynamic ability of the robot and motivate development of optimization algorithms able to take advantage of the robot's increased control authority.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge