Siddharth H. Nair
Scalable Multi-modal Model Predictive Control via Duality-based Interaction Predictions
Feb 02, 2024



Abstract:We propose a hierarchical architecture designed for scalable real-time Model Predictive Control (MPC) in complex, multi-modal traffic scenarios. This architecture comprises two key components: 1) RAID-Net, a novel attention-based Recurrent Neural Network that predicts relevant interactions along the MPC prediction horizon between the autonomous vehicle and the surrounding vehicles using Lagrangian duality, and 2) a reduced Stochastic MPC problem that eliminates irrelevant collision avoidance constraints, enhancing computational efficiency. Our approach is demonstrated in a simulated traffic intersection with interactive surrounding vehicles, showcasing a 12x speed-up in solving the motion planning problem. A video demonstrating the proposed architecture in multiple complex traffic scenarios can be found here: https://youtu.be/-TcMeolCLWc
Predictive Control for Autonomous Driving with Uncertain, Multi-modal Predictions
Oct 31, 2023



Abstract:We propose a Stochastic MPC (SMPC) formulation for path planning with autonomous vehicles in scenarios involving multiple agents with multi-modal predictions. The multi-modal predictions capture the uncertainty of urban driving in distinct modes/maneuvers (e.g., yield, keep speed) and driving trajectories (e.g., speed, turning radius), which are incorporated for multi-modal collision avoidance chance constraints for path planning. In the presence of multi-modal uncertainties, it is challenging to reliably compute feasible path planning solutions at real-time frequencies ($\geq$ 10 Hz). Our main technological contribution is a convex SMPC formulation that simultaneously (1) optimizes over parameterized feedback policies and (2) allocates risk levels for each mode of the prediction. The use of feedback policies and risk allocation enhances the feasibility and performance of the SMPC formulation against multi-modal predictions with large uncertainty. We evaluate our approach via simulations and road experiments with a full-scale vehicle interacting in closed-loop with virtual vehicles. We consider distinct, multi-modal driving scenarios: 1) Negotiating a traffic light and a fast, tailgating agent, 2) Executing an unprotected left turn at a traffic intersection, and 3) Changing lanes in the presence of multiple agents. For all of these scenarios, our approach reliably computes multi-modal solutions to the path-planning problem at real-time frequencies.
Interaction and Decision Making-aware Motion Planning using Branch Model Predictive Control
Jan 31, 2023



Abstract:Motion planning for autonomous vehicles sharing the road with human drivers remains challenging. The difficulty arises from three challenging aspects: human drivers are 1) multi-modal, 2) interacting with the autonomous vehicle, and 3) actively making decisions based on the current state of the traffic scene. We propose a motion planning framework based on Branch Model Predictive Control to deal with these challenges. The multi-modality is addressed by considering multiple future outcomes associated with different decisions taken by the human driver. The interactive nature of humans is considered by modeling them as reactive agents impacted by the actions of the autonomous vehicle. Finally, we consider a model developed in human neuroscience studies as a possible way of encoding the decision making process of human drivers. We present simulation results in various scenarios, showing the advantages of the proposed method and its ability to plan assertive maneuvers that convey intent to humans.
Collision Avoidance for Dynamic Obstacles with Uncertain Predictions using Model Predictive Control
Aug 06, 2022
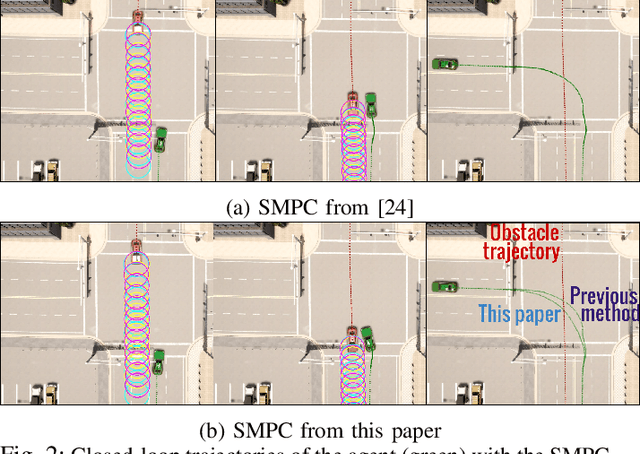

Abstract:We propose a Model Predictive Control (MPC) for collision avoidance between an autonomous agent and dynamic obstacles with uncertain predictions. The collision avoidance constraints are imposed by enforcing positive distance between convex sets representing the agent and the obstacles, and tractably reformulating them using Lagrange duality. This approach allows for smooth collision avoidance constraints even for polytopes, which otherwise require mixed-integer or non-smooth constraints. We consider three widely used descriptions of the uncertain obstacle position: 1) Arbitrary distribution with polytopic support, 2) Gaussian distributions and 3) Arbitrary distribution with first two moments known. For each case we obtain deterministic reformulations of the collision avoidance constraints. The proposed MPC formulation optimizes over feedback policies to reduce conservatism in satisfying the collision avoidance constraints. The proposed approach is validated using simulations of traffic intersections in CARLA.
Stochastic MPC with Multi-modal Predictions for Traffic Intersections
Sep 26, 2021
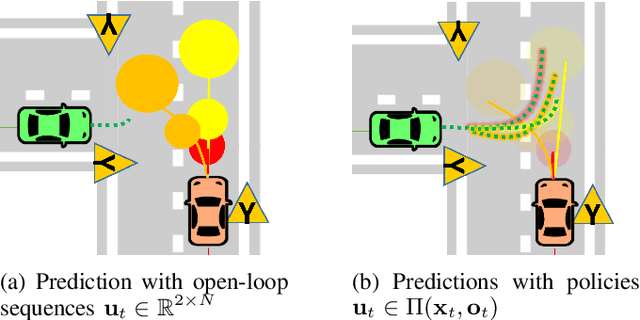
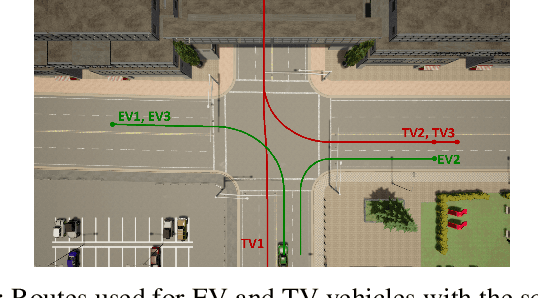
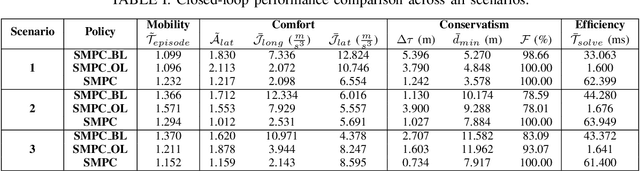
Abstract:We propose a Stochastic MPC (SMPC) formulation for autonomous driving at traffic intersections which incorporates multi-modal predictions of surrounding vehicles for collision avoidance constraints. The multi-modal predictions are obtained with Gaussian Mixture Models (GMM) and constraints are formulated as chance-constraints. Our main theoretical contribution is a SMPC formulation that optimizes over a novel feedback policy class designed to exploit additional structure in the GMM predictions, and that is amenable to convex programming. The use of feedback policies for prediction is motivated by the need for reduced conservatism in handling multi-modal predictions of the surrounding vehicles, especially prevalent in traffic intersection scenarios. We evaluate our algorithm along axes of mobility, comfort, conservatism and computational efficiency at a simulated intersection in CARLA. Our simulations use a kinematic bicycle model and multimodal predictions trained on a subset of the Lyft Level 5 prediction dataset. To demonstrate the impact of optimizing over feedback policies, we compare our algorithm with two SMPC baselines that handle multi-modal collision avoidance chance constraints by optimizing over open-loop sequences.
Predictive Control for Chasing a Ground Vehicle using a UAV
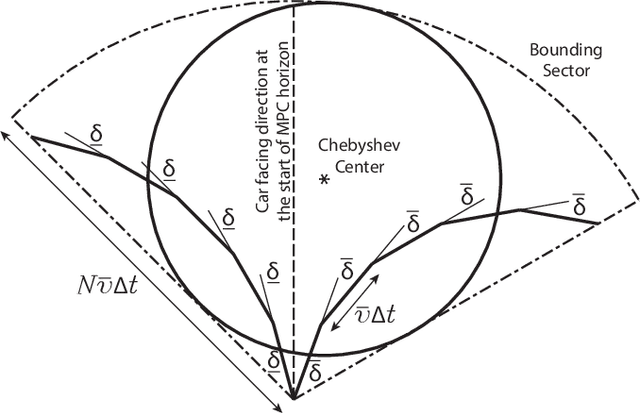
May 22, 2019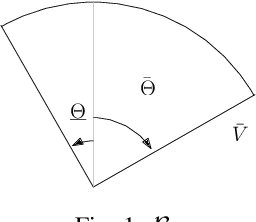

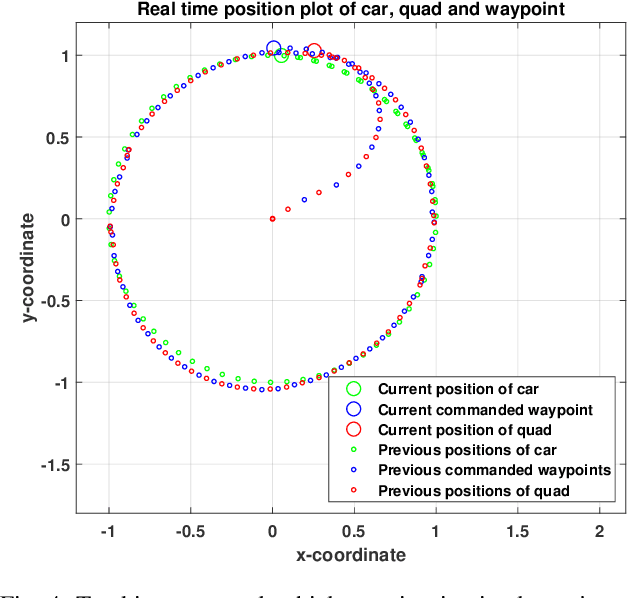
Abstract:We propose a high-level planner for a multirotor to chase a ground vehicle, while simultaneously respecting various state and input constraints. Assuming a minimal kinematic model for the ground vehicle, we use data collected online to generate predictions for our planner within a model predictive control framework. Our solution is demonstrated, both via simulations and experiments on a stable quadcopter platform.
Hilbert's Space-filling Curve for Regions with Holes
Sep 09, 2017
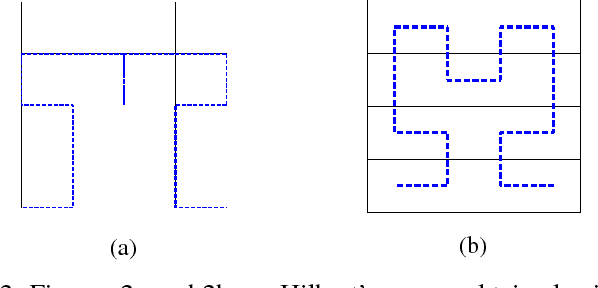
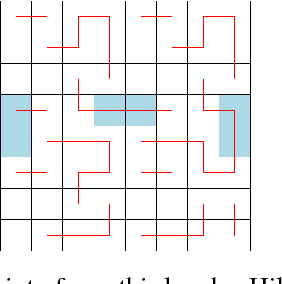

Abstract:The paper presents a systematic strategy for implementing Hilbert's space filling curve for use in online exploration tasks and addresses its application in scenarios wherein the space to be searched obstacles (or holes) whose locations are not known a priori. Using the self-similarity and locality preserving properties of Hilbert's space filling curve, a set of evasive maneuvers are prescribed and characterized for online implementation. Application of these maneuvers in the case of non-uniform coverage of spaces and for obstacles of varying sizes is also presented. The results are validated with representative simulations demonstrating the deployment of the approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge