Data-Driven Optimization for Deposition with Degradable Tools

We present a data-driven optimization approach for robotic controlled deposition with a degradable tool. Existing methods make the assumption that the tool tip is not changing or is replaced frequently. Errors can accumulate over time as the tool wears away and this leads to poor performance in the case where the tool degradation is unaccounted for during deposition. In the proposed approach, we utilize visual and force feedback to update the unknown model parameters of our tool-tip. Subsequently, we solve a constrained finite time optimal control problem for tracking a reference deposition profile, where our robot plans with the learned tool degradation dynamics. We focus on a robotic drawing problem as an illustrative example. Using real-world experiments, we show that the error in target vs actual deposition decreases when learned degradation models are used in the control design.

Safe Human-Robot Collaborative Transportation via Trust-Driven Role Adaptation

We study a human-robot collaborative transportation task in presence of obstacles. The task for each agent is to carry a rigid object to a common target position, while safely avoiding obstacles and satisfying the compliance and actuation constraints of the other agent. Human and robot do not share the local view of the environment. The human policy either assists the robot when they deem the robot actions safe based on their perception of the environment, or actively leads the task. Using estimated human inputs, the robot plans a trajectory for the transported object by solving a constrained finite time optimal control problem. Sensors on the robot measure the inputs applied by the human. The robot then appropriately applies a weighted combination of the human's applied and its own planned inputs, where the weights are chosen based on the robot's trust value on its estimates of the human's inputs. This allows for a dynamic leader-follower role adaptation of the robot throughout the task. Furthermore, under a low value of trust, if the robot approaches any obstacle potentially unknown to the human, it triggers a safe stopping policy, maintaining safety of the system and signaling a required change in the human's intent. With experimental results, we demonstrate the efficacy of the proposed approach.

Decentralized 2-Robot Transportation with Local and Indirect Sensing

In this paper, we propose a leader-follower hierarchical strategy for two robots collaboratively transporting an object in a partially known environment with obstacles. Both robots sense the local surrounding environment and react to obstacles in their proximity. We consider no explicit communication, so the local environment information and the control actions are not shared between the robots. At any given time step, the leader solves a model predictive control (MPC) problem with its known set of obstacles and plans a feasible trajectory to complete the task. The follower estimates the inputs of the leader and uses a policy to assist the leader while reacting to obstacles in its proximity. The leader infers obstacles in the follower's vicinity by using the difference between the predicted and the real-time estimated follower control action. A method to switch the leader-follower roles is used to improve the control performance in tight environments. The efficacy of our approach is demonstrated with detailed comparisons to two alternative strategies, where it achieves the highest success rate, while completing the task fastest.

Learning How to Solve Bubble Ball

"Bubble Ball" is a game built on a 2D physics engine, where a finite set of objects can modify the motion of a bubble-like ball. The objective is to choose the set and the initial configuration of the objects, in order to get the ball to reach a target flag. The presence of obstacles, friction, contact forces and combinatorial object choices make the game hard to solve. In this paper, we propose a hierarchical predictive framework which solves Bubble Ball. Geometric, kinematic and dynamic models are used at different levels of the hierarchy. At each level of the game, data collected during failed iterations are used to update models at all hierarchical level and converge to a feasible solution to the game. The proposed approach successfully solves a large set of Bubble Ball levels within reasonable number of trials. This proposed framework can also be used to solve other physics-based games, especially with limited training data from human demonstrations.

Traction Adaptive Motion Planning at the Limits of Handling

In this paper we address the problem of motion planning and control at the limits of handling, under locally varying traction conditions. We propose a novel solution method where locally varying traction is represented by time-varying tire force constraints. A constrained finite time optimal control problem is solved in a receding horizon fashion, imposing these time-varying constraints. Furthermore, we employ a sampling augmentation procedure to address the problems of infeasibility and sensitivity to local minima that arises when the constraint configuration is altered. We validate the proposed algorithm on a Volvo FH16 heavy-duty vehicle, in a range of critical scenarios. Experimental results indicate that traction adaptation improves the vehicle's capacity to avoid accidents, both when adapting to low and high local traction.

Learning to Play Cup-and-Ball with Noisy Camera Observations

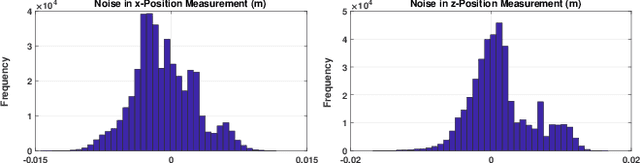
Playing the cup-and-ball game is an intriguing task for robotics research since it abstracts important problem characteristics including system nonlinearity, contact forces and precise positioning as terminal goal. In this paper, we present a learning model based control strategy for the cup-and-ball game, where a Universal Robots UR5e manipulator arm learns to catch a ball in one of the cups on a Kendama. Our control problem is divided into two sub-tasks, namely $(i)$ swinging the ball up in a constrained motion, and $(ii)$ catching the free-falling ball. The swing-up trajectory is computed offline, and applied in open-loop to the arm. Subsequently, a convex optimization problem is solved online during the ball's free-fall to control the manipulator and catch the ball. The controller utilizes noisy position feedback of the ball from an Intel RealSense D435 depth camera. We propose a novel iterative framework, where data is used to learn the support of the camera noise distribution iteratively in order to update the control policy. The probability of a catch with a fixed policy is computed empirically with a user specified number of roll-outs. Our design guarantees that probability of the catch increases in the limit, as the learned support nears the true support of the camera noise distribution. High-fidelity Mujoco simulations and preliminary experimental results support our theoretical analysis.

Learning to Satisfy Unknown Constraints in Iterative MPC

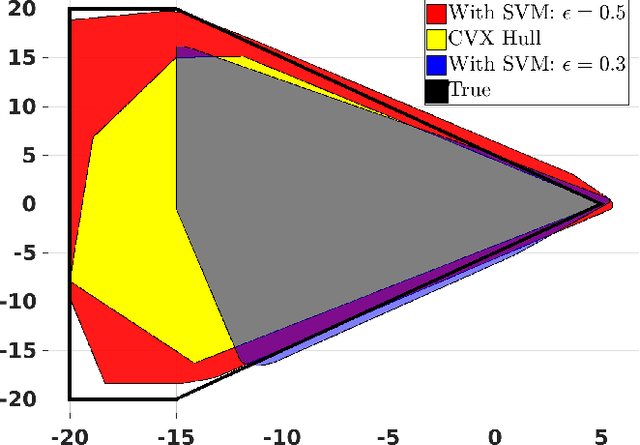
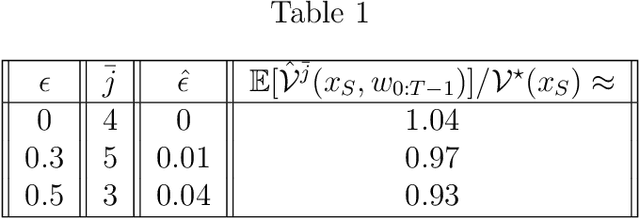
We propose a control design method for linear time-invariant systems that iteratively learns to satisfy unknown polyhedral state constraints. At each iteration of a repetitive task, the method constructs an estimate of the unknown environment constraints using collected closed-loop trajectory data. This estimated constraint set is improved iteratively upon collection of additional data. An MPC controller is then designed to robustly satisfy the estimated constraint set. This paper presents the details of the proposed approach, and provides robust and probabilistic guarantees of constraint satisfaction as a function of the number of executed task iterations. We demonstrate the efficacy of the proposed framework in a detailed numerical example.

Exploiting Model Sparsity in Adaptive MPC: A Compressed Sensing Viewpoint

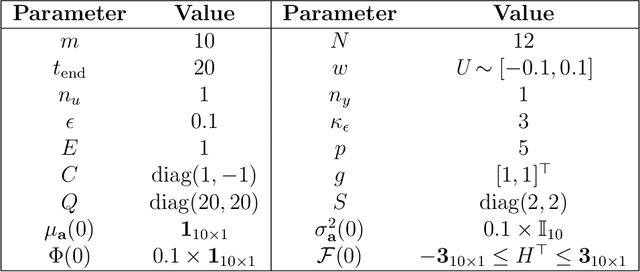
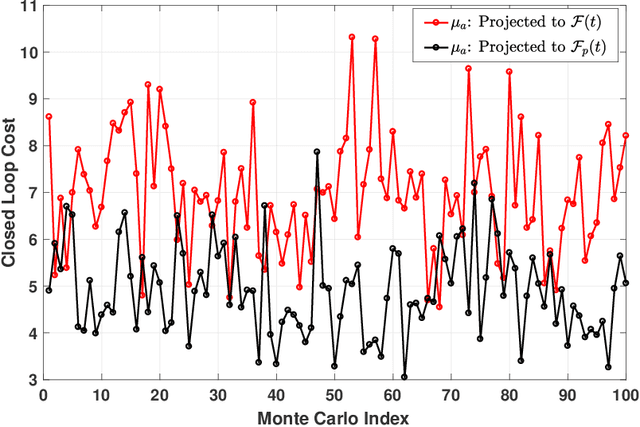
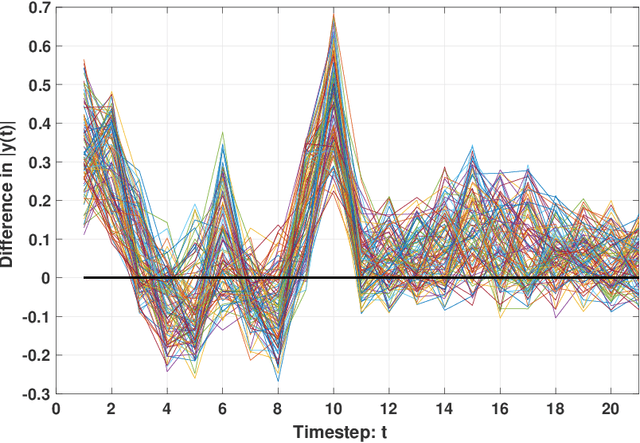
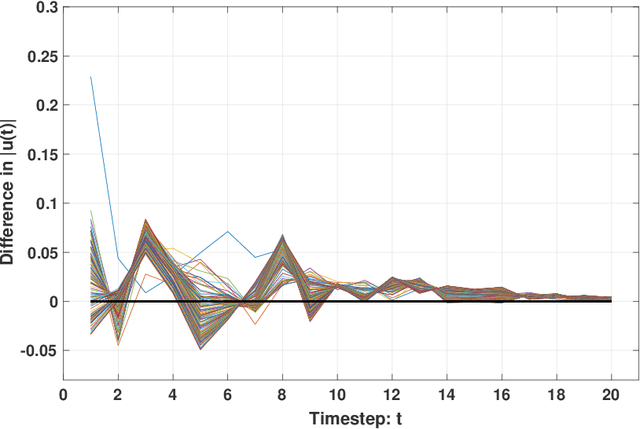
This paper proposes an Adaptive Stochastic Model Predictive Control (MPC) strategy for stable linear time-invariant systems in the presence of bounded disturbances. We consider multi-input, multi-output systems that can be expressed by a Finite Impulse Response (FIR) model. The parameters of the FIR model corresponding to each output are unknown but assumed sparse. We estimate these parameters using the Recursive Least Squares algorithm. The estimates are then improved using set-based bounds obtained by solving the Basis Pursuit Denoising [1] problem. Our approach is able to handle hard input constraints and probabilistic output constraints. Using tools from distributionally robust optimization, we reformulate the probabilistic output constraints as tractable convex second-order cone constraints, which enables us to pose our MPC design task as a convex optimization problem. The efficacy of the developed algorithm is highlighted with a thorough numerical example, where we demonstrate performance gain over the counterpart algorithm of [2], which does not utilize the sparsity information of the system impulse response parameters during control design.

Generalized Policy Iteration for Optimal Control in Continuous Time

This paper proposes the Deep Generalized Policy Iteration (DGPI) algorithm to find the infinite horizon optimal control policy for general nonlinear continuous-time systems with known dynamics. Unlike existing adaptive dynamic programming algorithms for continuous time systems, DGPI does not require the admissibility of initialized policy, and input-affine nature of controlled systems for convergence. Our algorithm employs the actor-critic architecture to approximate both policy and value functions with the purpose of iteratively solving the Hamilton-Jacobi-Bellman equation. Both the policy and value functions are approximated by deep neural networks. Given any arbitrary initial policy, the proposed DGPI algorithm can eventually converge to an admissible, and subsequently an optimal policy for an arbitrary nonlinear system. We also relax the update termination conditions of both the policy evaluation and improvement processes, which leads to a faster convergence speed than conventional Policy Iteration (PI) methods, for the same architecture of function approximators. We further prove the convergence and optimality of the algorithm with thorough Lyapunov analysis, and demonstrate its generality and efficacy using two detailed numerical examples.

Safe and Near-Optimal Policy Learning for Model Predictive Control using Primal-Dual Neural Networks

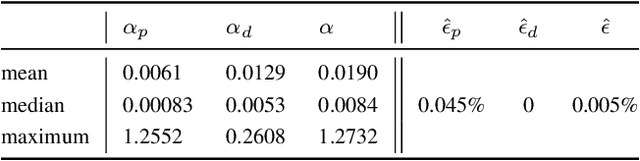
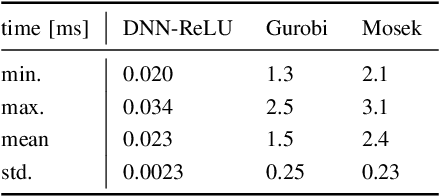
In this paper, we propose a novel framework for approximating the explicit MPC law for linear parameter-varying systems using supervised learning. In contrast to most existing approaches, we not only learn the control policy, but also a "certificate policy", that allows us to estimate the sub-optimality of the learned control policy online, during execution-time. We learn both these policies from data using supervised learning techniques, and also provide a randomized method that allows us to guarantee the quality of each learned policy, measured in terms of feasibility and optimality. This in turn allows us to bound the probability of the learned control policy of being infeasible or suboptimal, where the check is performed by the certificate policy. Since our algorithm does not require the solution of an optimization problem during run-time, it can be deployed even on resource-constrained systems. We illustrate the efficacy of the proposed framework on a vehicle dynamics control problem where we demonstrate a speedup of up to two orders of magnitude compared to online optimization with minimal performance degradation.