Stochastic convex optimization for provably efficient apprenticeship learning

We consider large-scale Markov decision processes (MDPs) with an unknown cost function and employ stochastic convex optimization tools to address the problem of imitation learning, which consists of learning a policy from a finite set of expert demonstrations. We adopt the apprenticeship learning formalism, which carries the assumption that the true cost function can be represented as a linear combination of some known features. Existing inverse reinforcement learning algorithms come with strong theoretical guarantees, but are computationally expensive because they use reinforcement learning or planning algorithms as a subroutine. On the other hand, state-of-the-art policy gradient based algorithms (like IM-REINFORCE, IM-TRPO, and GAIL), achieve significant empirical success in challenging benchmark tasks, but are not well understood in terms of theory. With an emphasis on non-asymptotic guarantees of performance, we propose a method that directly learns a policy from expert demonstrations, bypassing the intermediate step of learning the cost function, by formulating the problem as a single convex optimization problem over occupancy measures. We develop a computationally efficient algorithm and derive high confidence regret bounds on the quality of the extracted policy, utilizing results from stochastic convex optimization and recent works in approximate linear programming for solving forward MDPs.

Efficient Performance Bounds for Primal-Dual Reinforcement Learning from Demonstrations

We consider large-scale Markov decision processes with an unknown cost function and address the problem of learning a policy from a finite set of expert demonstrations. We assume that the learner is not allowed to interact with the expert and has no access to reinforcement signal of any kind. Existing inverse reinforcement learning methods come with strong theoretical guarantees, but are computationally expensive, while state-of-the-art policy optimization algorithms achieve significant empirical success, but are hampered by limited theoretical understanding. To bridge the gap between theory and practice, we introduce a novel bilinear saddle-point framework using Lagrangian duality. The proposed primal-dual viewpoint allows us to develop a model-free provably efficient algorithm through the lens of stochastic convex optimization. The method enjoys the advantages of simplicity of implementation, low memory requirements, and computational and sample complexities independent of the number of states. We further present an equivalent no-regret online-learning interpretation.

Accelerating Quadratic Optimization with Reinforcement Learning

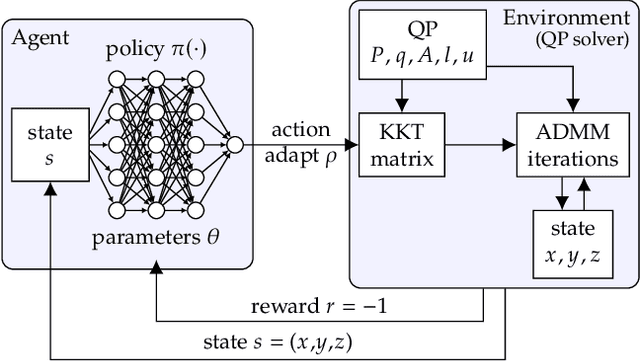
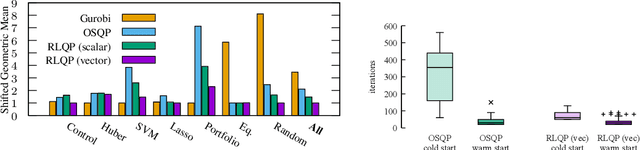
First-order methods for quadratic optimization such as OSQP are widely used for large-scale machine learning and embedded optimal control, where many related problems must be rapidly solved. These methods face two persistent challenges: manual hyperparameter tuning and convergence time to high-accuracy solutions. To address these, we explore how Reinforcement Learning (RL) can learn a policy to tune parameters to accelerate convergence. In experiments with well-known QP benchmarks we find that our RL policy, RLQP, significantly outperforms state-of-the-art QP solvers by up to 3x. RLQP generalizes surprisingly well to previously unseen problems with varying dimension and structure from different applications, including the QPLIB, Netlib LP and Maros-Meszaros problems. Code for RLQP is available at https://github.com/berkeleyautomation/rlqp.