Randomized algorithms and PAC bounds for inverse reinforcement learning in continuous spaces

This work studies discrete-time discounted Markov decision processes with continuous state and action spaces and addresses the inverse problem of inferring a cost function from observed optimal behavior. We first consider the case in which we have access to the entire expert policy and characterize the set of solutions to the inverse problem by using occupation measures, linear duality, and complementary slackness conditions. To avoid trivial solutions and ill-posedness, we introduce a natural linear normalization constraint. This results in an infinite-dimensional linear feasibility problem, prompting a thorough analysis of its properties. Next, we use linear function approximators and adopt a randomized approach, namely the scenario approach and related probabilistic feasibility guarantees, to derive epsilon-optimal solutions for the inverse problem. We further discuss the sample complexity for a desired approximation accuracy. Finally, we deal with the more realistic case where we only have access to a finite set of expert demonstrations and a generative model and provide bounds on the error made when working with samples.

Proximal Point Imitation Learning

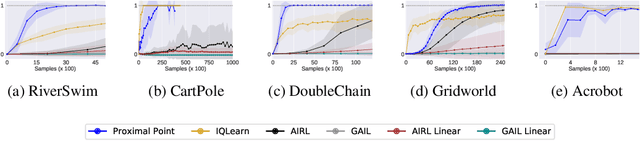
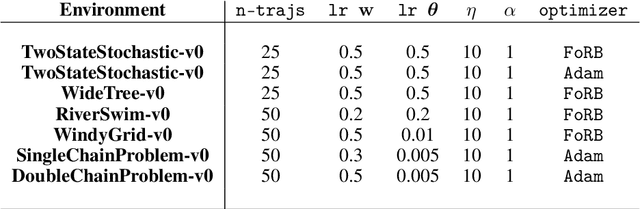
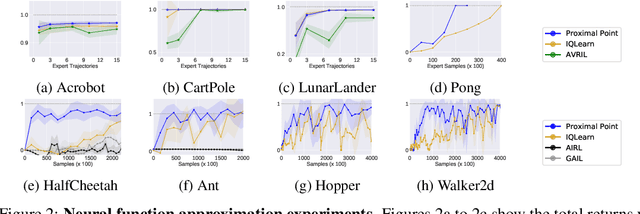
This work develops new algorithms with rigorous efficiency guarantees for infinite horizon imitation learning (IL) with linear function approximation without restrictive coherence assumptions. We begin with the minimax formulation of the problem and then outline how to leverage classical tools from optimization, in particular, the proximal-point method (PPM) and dual smoothing, for online and offline IL, respectively. Thanks to PPM, we avoid nested policy evaluation and cost updates for online IL appearing in the prior literature. In particular, we do away with the conventional alternating updates by the optimization of a single convex and smooth objective over both cost and Q-functions. When solved inexactly, we relate the optimization errors to the suboptimality of the recovered policy. As an added bonus, by re-interpreting PPM as dual smoothing with the expert policy as a center point, we also obtain an offline IL algorithm enjoying theoretical guarantees in terms of required expert trajectories. Finally, we achieve convincing empirical performance for both linear and neural network function approximation.

Stochastic convex optimization for provably efficient apprenticeship learning

We consider large-scale Markov decision processes (MDPs) with an unknown cost function and employ stochastic convex optimization tools to address the problem of imitation learning, which consists of learning a policy from a finite set of expert demonstrations. We adopt the apprenticeship learning formalism, which carries the assumption that the true cost function can be represented as a linear combination of some known features. Existing inverse reinforcement learning algorithms come with strong theoretical guarantees, but are computationally expensive because they use reinforcement learning or planning algorithms as a subroutine. On the other hand, state-of-the-art policy gradient based algorithms (like IM-REINFORCE, IM-TRPO, and GAIL), achieve significant empirical success in challenging benchmark tasks, but are not well understood in terms of theory. With an emphasis on non-asymptotic guarantees of performance, we propose a method that directly learns a policy from expert demonstrations, bypassing the intermediate step of learning the cost function, by formulating the problem as a single convex optimization problem over occupancy measures. We develop a computationally efficient algorithm and derive high confidence regret bounds on the quality of the extracted policy, utilizing results from stochastic convex optimization and recent works in approximate linear programming for solving forward MDPs.

Efficient Performance Bounds for Primal-Dual Reinforcement Learning from Demonstrations

We consider large-scale Markov decision processes with an unknown cost function and address the problem of learning a policy from a finite set of expert demonstrations. We assume that the learner is not allowed to interact with the expert and has no access to reinforcement signal of any kind. Existing inverse reinforcement learning methods come with strong theoretical guarantees, but are computationally expensive, while state-of-the-art policy optimization algorithms achieve significant empirical success, but are hampered by limited theoretical understanding. To bridge the gap between theory and practice, we introduce a novel bilinear saddle-point framework using Lagrangian duality. The proposed primal-dual viewpoint allows us to develop a model-free provably efficient algorithm through the lens of stochastic convex optimization. The method enjoys the advantages of simplicity of implementation, low memory requirements, and computational and sample complexities independent of the number of states. We further present an equivalent no-regret online-learning interpretation.