Adaptive Optimization for Prediction with Missing Data

When training predictive models on data with missing entries, the most widely used and versatile approach is a pipeline technique where we first impute missing entries and then compute predictions. In this paper, we view prediction with missing data as a two-stage adaptive optimization problem and propose a new class of models, adaptive linear regression models, where the regression coefficients adapt to the set of observed features. We show that some adaptive linear regression models are equivalent to learning an imputation rule and a downstream linear regression model simultaneously instead of sequentially. We leverage this joint-impute-then-regress interpretation to generalize our framework to non-linear models. In settings where data is strongly not missing at random, our methods achieve a 2-10% improvement in out-of-sample accuracy.

Solving the Quadratic Assignment Problem using Deep Reinforcement Learning

The Quadratic Assignment Problem (QAP) is an NP-hard problem which has proven particularly challenging to solve: unlike other combinatorial problems like the traveling salesman problem (TSP), which can be solved to optimality for instances with hundreds or even thousands of locations using advanced integer programming techniques, no methods are known to exactly solve QAP instances of size greater than 30. Solving the QAP is nevertheless important because of its many critical applications, such as electronic wiring design and facility layout selection. We propose a method to solve the original Koopmans-Beckman formulation of the QAP using deep reinforcement learning. Our approach relies on a novel double pointer network, which alternates between selecting a location in which to place the next facility and a facility to place in the previous location. We train our model using A2C on a large dataset of synthetic instances, producing solutions with no instance-specific retraining necessary. Out of sample, our solutions are on average within 7.5% of a high-quality local search baseline, and even outperform it on 1.2% of instances.

Prediction with Missing Data

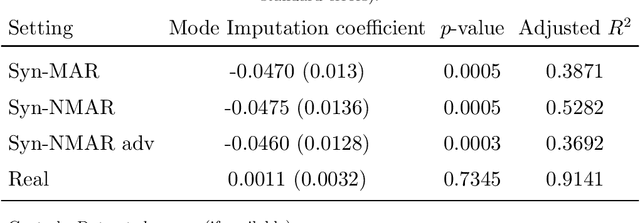
Missing information is inevitable in real-world data sets. While imputation is well-suited and theoretically sound for statistical inference, its relevance and practical implementation for out-of-sample prediction remains unsettled. We provide a theoretical analysis of widely used data imputation methods and highlight their key deficiencies in making accurate predictions. Alternatively, we propose adaptive linear regression, a new class of models that can be directly trained and evaluated on partially observed data, adapting to the set of available features. In particular, we show that certain adaptive regression models are equivalent to impute-then-regress methods where the imputation and the regression models are learned simultaneously instead of sequentially. We validate our theoretical findings and adaptive regression approach with numerical results with real-world data sets.

Reinforcement Learning with Combinatorial Actions: An Application to Vehicle Routing

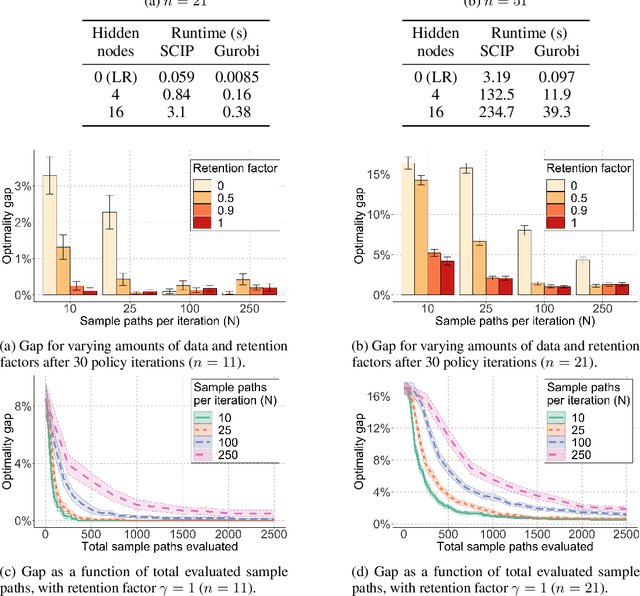
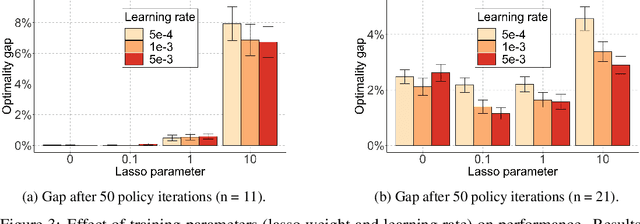
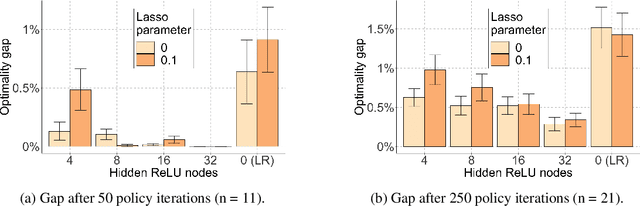
Value-function-based methods have long played an important role in reinforcement learning. However, finding the best next action given a value function of arbitrary complexity is nontrivial when the action space is too large for enumeration. We develop a framework for value-function-based deep reinforcement learning with a combinatorial action space, in which the action selection problem is explicitly formulated as a mixed-integer optimization problem. As a motivating example, we present an application of this framework to the capacitated vehicle routing problem (CVRP), a combinatorial optimization problem in which a set of locations must be covered by a single vehicle with limited capacity. On each instance, we model an action as the construction of a single route, and consider a deterministic policy which is improved through a simple policy iteration algorithm. Our approach is competitive with other reinforcement learning methods and achieves an average gap of 1.7% with state-of-the-art OR methods on standard library instances of medium size.

From predictions to prescriptions: A data-driven response to COVID-19

The COVID-19 pandemic has created unprecedented challenges worldwide. Strained healthcare providers make difficult decisions on patient triage, treatment and care management on a daily basis. Policy makers have imposed social distancing measures to slow the disease, at a steep economic price. We design analytical tools to support these decisions and combat the pandemic. Specifically, we propose a comprehensive data-driven approach to understand the clinical characteristics of COVID-19, predict its mortality, forecast its evolution, and ultimately alleviate its impact. By leveraging cohort-level clinical data, patient-level hospital data, and census-level epidemiological data, we develop an integrated four-step approach, combining descriptive, predictive and prescriptive analytics. First, we aggregate hundreds of clinical studies into the most comprehensive database on COVID-19 to paint a new macroscopic picture of the disease. Second, we build personalized calculators to predict the risk of infection and mortality as a function of demographics, symptoms, comorbidities, and lab values. Third, we develop a novel epidemiological model to project the pandemic's spread and inform social distancing policies. Fourth, we propose an optimization model to re-allocate ventilators and alleviate shortages. Our results have been used at the clinical level by several hospitals to triage patients, guide care management, plan ICU capacity, and re-distribute ventilators. At the policy level, they are currently supporting safe back-to-work policies at a major institution and equitable vaccine distribution planning at a major pharmaceutical company, and have been integrated into the US Center for Disease Control's pandemic forecast.

Optimal Explanations of Linear Models

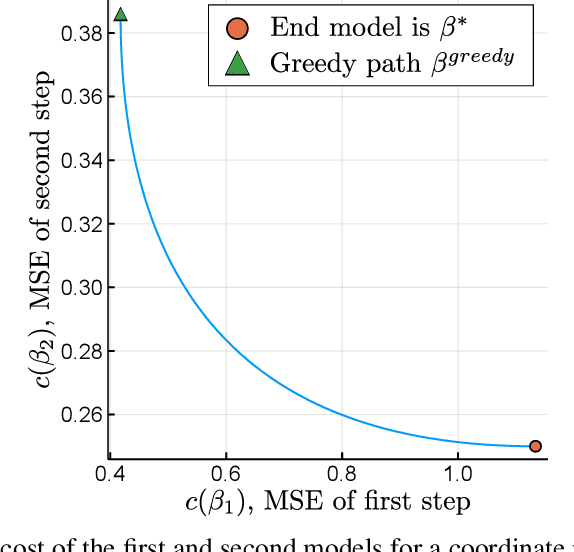
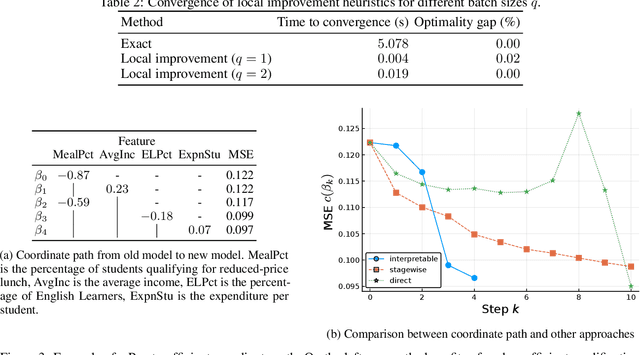
When predictive models are used to support complex and important decisions, the ability to explain a model's reasoning can increase trust, expose hidden biases, and reduce vulnerability to adversarial attacks. However, attempts at interpreting models are often ad hoc and application-specific, and the concept of interpretability itself is not well-defined. We propose a general optimization framework to create explanations for linear models. Our methodology decomposes a linear model into a sequence of models of increasing complexity using coordinate updates on the coefficients. Computing this decomposition optimally is a difficult optimization problem for which we propose exact algorithms and scalable heuristics. By solving this problem, we can derive a parametrized family of interpretability metrics for linear models that generalizes typical proxies, and study the tradeoff between interpretability and predictive accuracy.

The Price of Interpretability

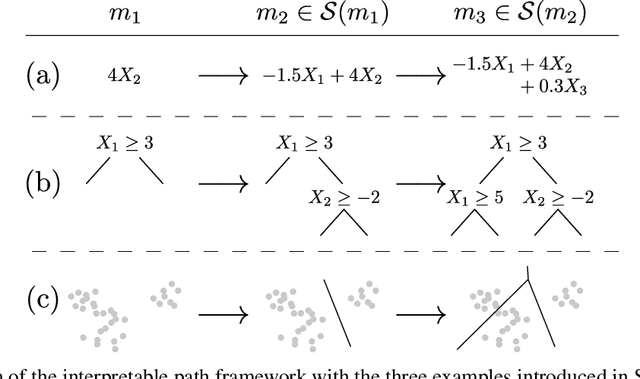
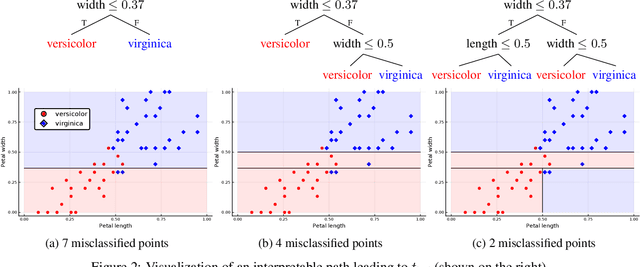
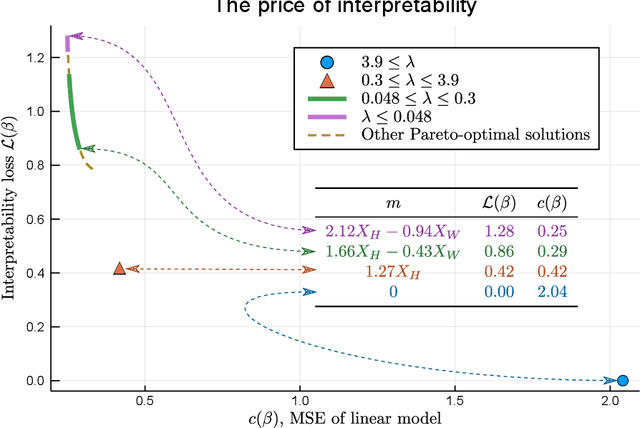
When quantitative models are used to support decision-making on complex and important topics, understanding a model's ``reasoning'' can increase trust in its predictions, expose hidden biases, or reduce vulnerability to adversarial attacks. However, the concept of interpretability remains loosely defined and application-specific. In this paper, we introduce a mathematical framework in which machine learning models are constructed in a sequence of interpretable steps. We show that for a variety of models, a natural choice of interpretable steps recovers standard interpretability proxies (e.g., sparsity in linear models). We then generalize these proxies to yield a parametrized family of consistent measures of model interpretability. This formal definition allows us to quantify the ``price'' of interpretability, i.e., the tradeoff with predictive accuracy. We demonstrate practical algorithms to apply our framework on real and synthetic datasets.