The Price of Interpretability
Paper and Code
Jul 08, 2019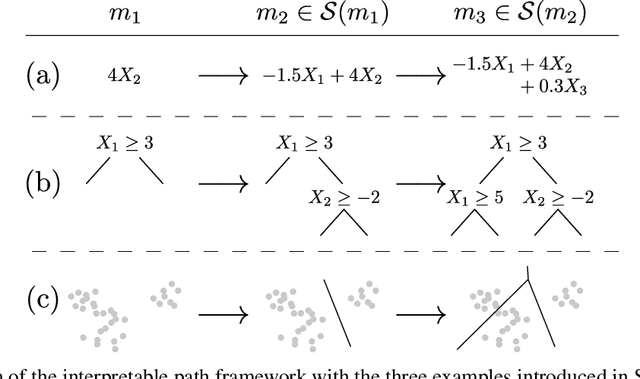

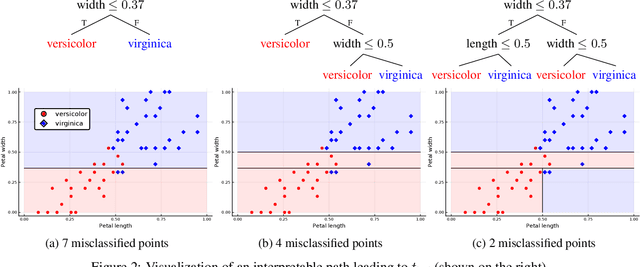

When quantitative models are used to support decision-making on complex and important topics, understanding a model's ``reasoning'' can increase trust in its predictions, expose hidden biases, or reduce vulnerability to adversarial attacks. However, the concept of interpretability remains loosely defined and application-specific. In this paper, we introduce a mathematical framework in which machine learning models are constructed in a sequence of interpretable steps. We show that for a variety of models, a natural choice of interpretable steps recovers standard interpretability proxies (e.g., sparsity in linear models). We then generalize these proxies to yield a parametrized family of consistent measures of model interpretability. This formal definition allows us to quantify the ``price'' of interpretability, i.e., the tradeoff with predictive accuracy. We demonstrate practical algorithms to apply our framework on real and synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge