Christian Tjandraatmadja
Solving Mixed Integer Programs Using Neural Networks
Dec 23, 2020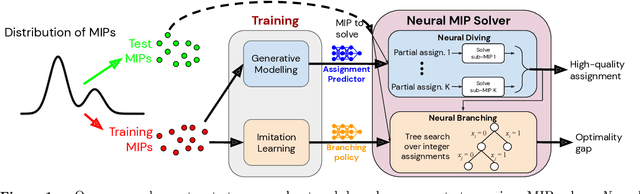
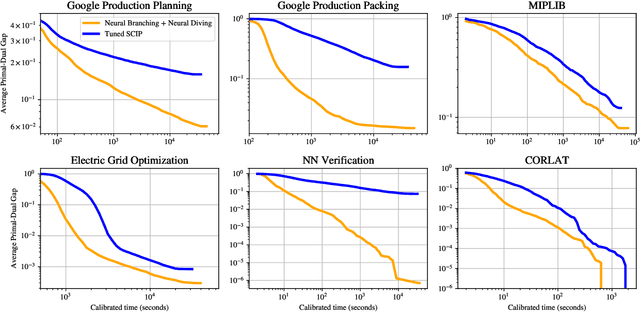
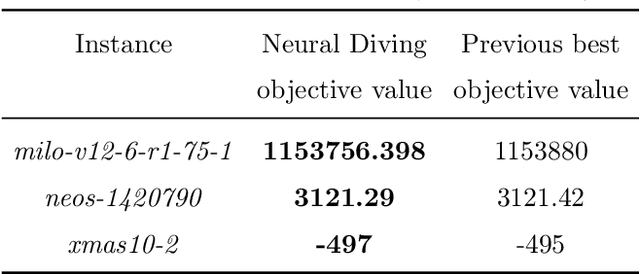
Abstract:Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.
Reinforcement Learning with Combinatorial Actions: An Application to Vehicle Routing
Oct 22, 2020
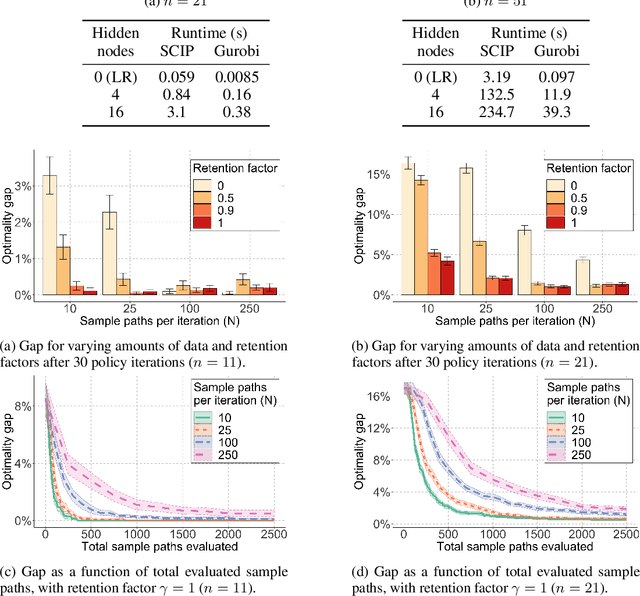
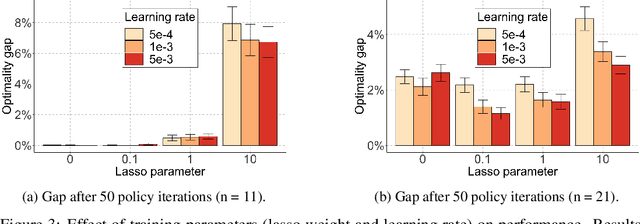
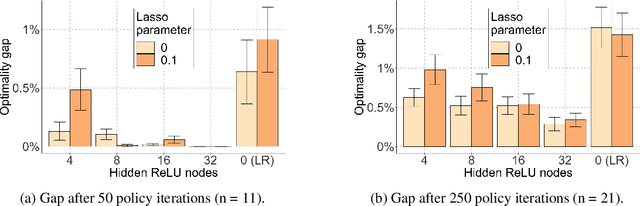
Abstract:Value-function-based methods have long played an important role in reinforcement learning. However, finding the best next action given a value function of arbitrary complexity is nontrivial when the action space is too large for enumeration. We develop a framework for value-function-based deep reinforcement learning with a combinatorial action space, in which the action selection problem is explicitly formulated as a mixed-integer optimization problem. As a motivating example, we present an application of this framework to the capacitated vehicle routing problem (CVRP), a combinatorial optimization problem in which a set of locations must be covered by a single vehicle with limited capacity. On each instance, we model an action as the construction of a single route, and consider a deterministic policy which is improved through a simple policy iteration algorithm. Our approach is competitive with other reinforcement learning methods and achieves an average gap of 1.7% with state-of-the-art OR methods on standard library instances of medium size.
The Convex Relaxation Barrier, Revisited: Tightened Single-Neuron Relaxations for Neural Network Verification
Jun 24, 2020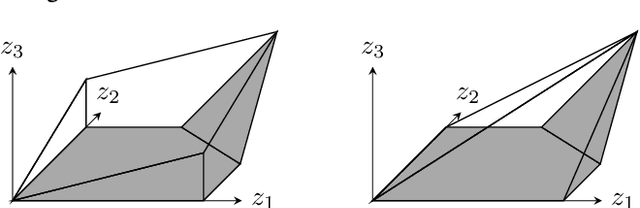
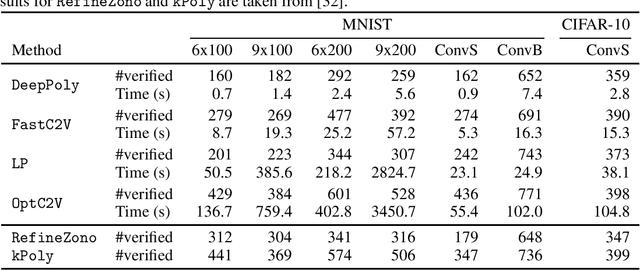
Abstract:We improve the effectiveness of propagation- and linear-optimization-based neural network verification algorithms with a new tightened convex relaxation for ReLU neurons. Unlike previous single-neuron relaxations which focus only on the univariate input space of the ReLU, our method considers the multivariate input space of the affine pre-activation function preceding the ReLU. Using results from submodularity and convex geometry, we derive an explicit description of the tightest possible convex relaxation when this multivariate input is over a box domain. We show that our convex relaxation is significantly stronger than the commonly used univariate-input relaxation which has been proposed as a natural convex relaxation barrier for verification. While our description of the relaxation may require an exponential number of inequalities, we show that they can be separated in linear time and hence can be efficiently incorporated into optimization algorithms on an as-needed basis. Based on this novel relaxation, we design two polynomial-time algorithms for neural network verification: a linear-programming-based algorithm that leverages the full power of our relaxation, and a fast propagation algorithm that generalizes existing approaches. In both cases, we show that for a modest increase in computational effort, our strengthened relaxation enables us to verify a significantly larger number of instances compared to similar algorithms.
CAQL: Continuous Action Q-Learning
Oct 09, 2019



Abstract:Value-based reinforcement learning (RL) methods like Q-learning have shown success in a variety of domains. One challenge in applying Q-learning to continuous-action RL problems, however, is the continuous action maximization (max-Q) required for optimal Bellman backup. In this work, we develop CAQL, a (class of) algorithm(s) for continuous-action Q-learning that can use several plug-and-play optimizers for the max-Q problem. Leveraging recent optimization results for deep neural networks, we show that max-Q can be solved optimally using mixed-integer programming (MIP). When the Q-function representation has sufficient power, MIP-based optimization gives rise to better policies and is more robust than approximate methods (e.g., gradient ascent, cross-entropy search). We further develop several techniques to accelerate inference in CAQL, which despite their approximate nature, perform well. We compare CAQL with state-of-the-art RL algorithms on benchmark continuous-control problems that have different degrees of action constraints and show that CAQL outperforms policy-based methods in heavily constrained environments, often dramatically.
Strong mixed-integer programming formulations for trained neural networks
Nov 20, 2018

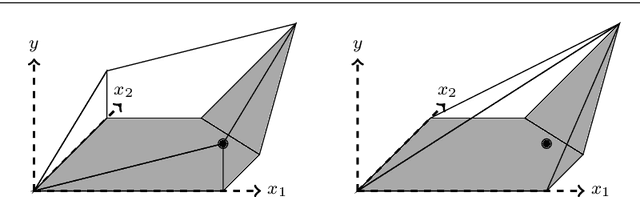

Abstract:We present an ideal mixed-integer programming (MIP) formulation for a rectified linear unit (ReLU) appearing in a trained neural network. Our formulation requires a single binary variable and no additional continuous variables beyond the input and output variables of the ReLU. We contrast it with an ideal "extended" formulation with a linear number of additional continuous variables, derived through standard techniques. An apparent drawback of our formulation is that it requires an exponential number of inequality constraints, but we provide a routine to separate the inequalities in linear time. We also prove that these exponentially-many constraints are facet-defining under mild conditions. Finally, we present computational results showing that dynamically separating from the exponential inequalities 1) is much more computationally efficient and scalable than the extended formulation, 2) decreases the solve time of a state-of-the-art MIP solver by a factor of 7 on smaller instances, and 3) nearly matches the dual bounds of a state-of-the-art MIP solver on harder instances, after just a few rounds of separation and in orders of magnitude less time.
Bounding and Counting Linear Regions of Deep Neural Networks
Sep 16, 2018



Abstract:We investigate the complexity of deep neural networks (DNN) that represent piecewise linear (PWL) functions. In particular, we study the number of linear regions, i.e. pieces, that a PWL function represented by a DNN can attain, both theoretically and empirically. We present (i) tighter upper and lower bounds for the maximum number of linear regions on rectifier networks, which are exact for inputs of dimension one; (ii) a first upper bound for multi-layer maxout networks; and (iii) a first method to perform exact enumeration or counting of the number of regions by modeling the DNN with a mixed-integer linear formulation. These bounds come from leveraging the dimension of the space defining each linear region. The results also indicate that a deep rectifier network can only have more linear regions than every shallow counterpart with same number of neurons if that number exceeds the dimension of the input.
How Could Polyhedral Theory Harness Deep Learning?
Jun 17, 2018Abstract:The holy grail of deep learning is to come up with an automatic method to design optimal architectures for different applications. In other words, how can we effectively dimension and organize neurons along the network layers based on the computational resources, input size, and amount of training data? We outline promising research directions based on polyhedral theory and mixed-integer representability that may offer an analytical approach to this question, in contrast to the empirical techniques often employed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge