The Convex Relaxation Barrier, Revisited: Tightened Single-Neuron Relaxations for Neural Network Verification

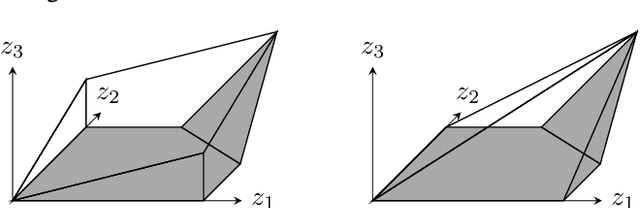
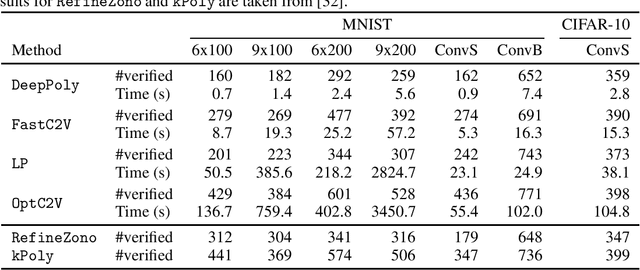
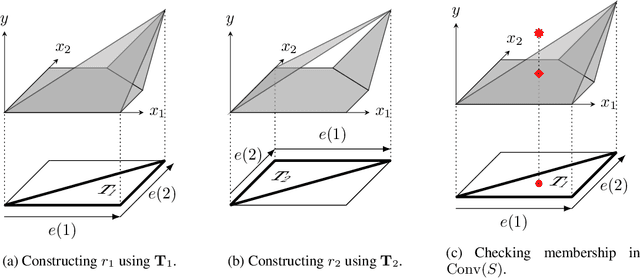
We improve the effectiveness of propagation- and linear-optimization-based neural network verification algorithms with a new tightened convex relaxation for ReLU neurons. Unlike previous single-neuron relaxations which focus only on the univariate input space of the ReLU, our method considers the multivariate input space of the affine pre-activation function preceding the ReLU. Using results from submodularity and convex geometry, we derive an explicit description of the tightest possible convex relaxation when this multivariate input is over a box domain. We show that our convex relaxation is significantly stronger than the commonly used univariate-input relaxation which has been proposed as a natural convex relaxation barrier for verification. While our description of the relaxation may require an exponential number of inequalities, we show that they can be separated in linear time and hence can be efficiently incorporated into optimization algorithms on an as-needed basis. Based on this novel relaxation, we design two polynomial-time algorithms for neural network verification: a linear-programming-based algorithm that leverages the full power of our relaxation, and a fast propagation algorithm that generalizes existing approaches. In both cases, we show that for a modest increase in computational effort, our strengthened relaxation enables us to verify a significantly larger number of instances compared to similar algorithms.

Strong mixed-integer programming formulations for trained neural networks

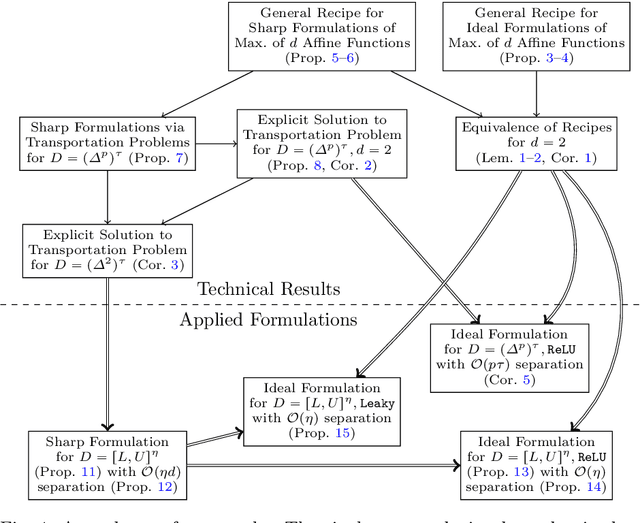
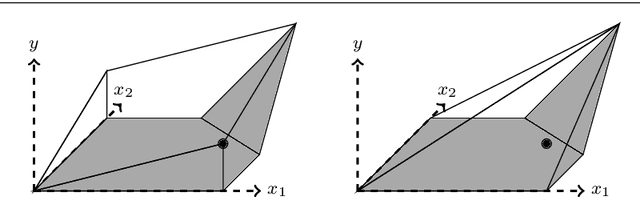
We present an ideal mixed-integer programming (MIP) formulation for a rectified linear unit (ReLU) appearing in a trained neural network. Our formulation requires a single binary variable and no additional continuous variables beyond the input and output variables of the ReLU. We contrast it with an ideal "extended" formulation with a linear number of additional continuous variables, derived through standard techniques. An apparent drawback of our formulation is that it requires an exponential number of inequality constraints, but we provide a routine to separate the inequalities in linear time. We also prove that these exponentially-many constraints are facet-defining under mild conditions. Finally, we present computational results showing that dynamically separating from the exponential inequalities 1) is much more computationally efficient and scalable than the extended formulation, 2) decreases the solve time of a state-of-the-art MIP solver by a factor of 7 on smaller instances, and 3) nearly matches the dual bounds of a state-of-the-art MIP solver on harder instances, after just a few rounds of separation and in orders of magnitude less time.