Ivan Lobov
Solving MaxSAT with Matrix Multiplication
Nov 01, 2023
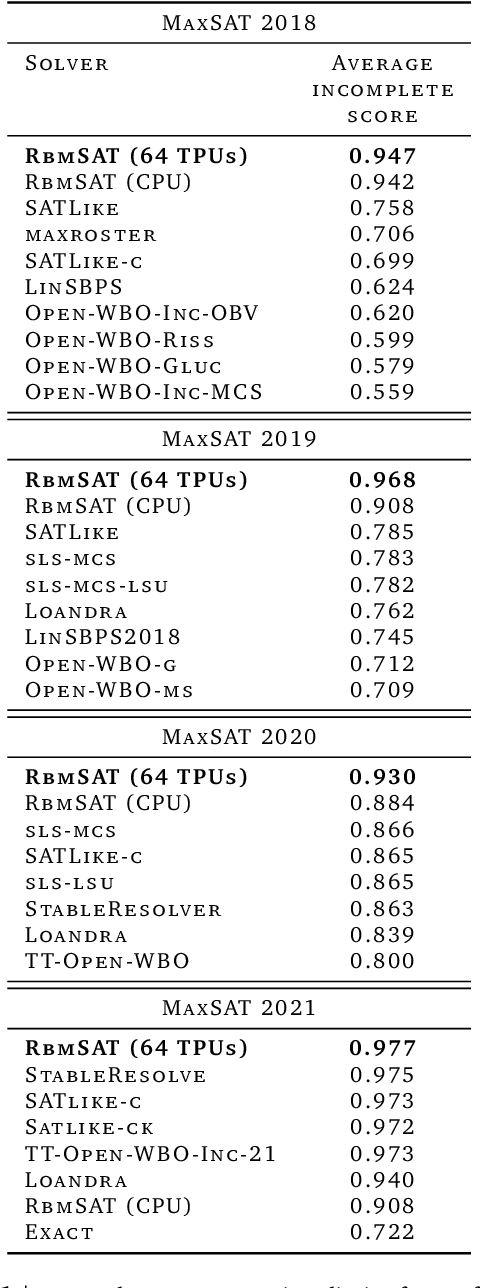


Abstract:We propose an incomplete algorithm for Maximum Satisfiability (MaxSAT) specifically designed to run on neural network accelerators such as GPUs and TPUs. Given a MaxSAT problem instance in conjunctive normal form, our procedure constructs a Restricted Boltzmann Machine (RBM) with an equilibrium distribution wherein the probability of a Boolean assignment is exponential in the number of clauses it satisfies. Block Gibbs sampling is used to stochastically search the space of assignments with parallel Markov chains. Since matrix multiplication is the main computational primitive for block Gibbs sampling in an RBM, our approach leads to an elegantly simple algorithm (40 lines of JAX) well-suited for neural network accelerators. Theoretical results about RBMs guarantee that the required number of visible and hidden units of the RBM scale only linearly with the number of variables and constant-sized clauses in the MaxSAT instance, ensuring that the computational cost of a Gibbs step scales reasonably with the instance size. Search throughput can be increased by batching parallel chains within a single accelerator as well as by distributing them across multiple accelerators. As a further enhancement, a heuristic based on unit propagation running on CPU is periodically applied to the sampled assignments. Our approach, which we term RbmSAT, is a new design point in the algorithm-hardware co-design space for MaxSAT. We present timed results on a subset of problem instances from the annual MaxSAT Evaluation's Incomplete Unweighted Track for the years 2018 to 2021. When allotted the same running time and CPU compute budget (but no TPUs), RbmSAT outperforms other participating solvers on problems drawn from three out of the four years' competitions. Given the same running time on a TPU cluster for which RbmSAT is uniquely designed, it outperforms all solvers on problems drawn from all four years.
Solving Mixed Integer Programs Using Neural Networks
Dec 23, 2020
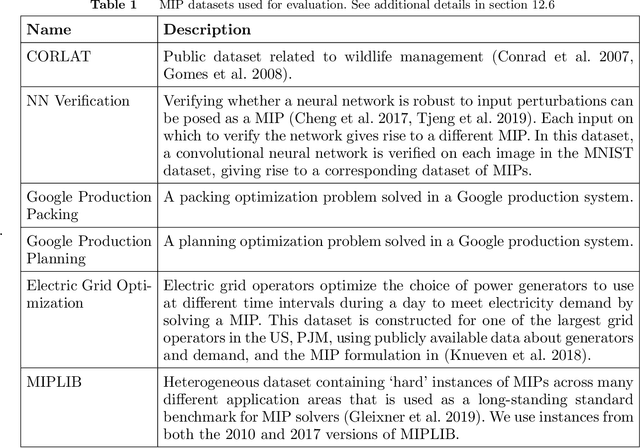
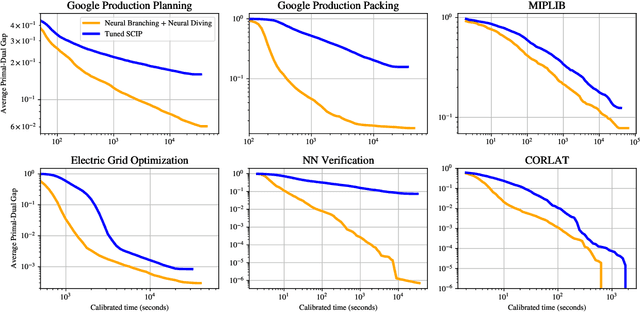
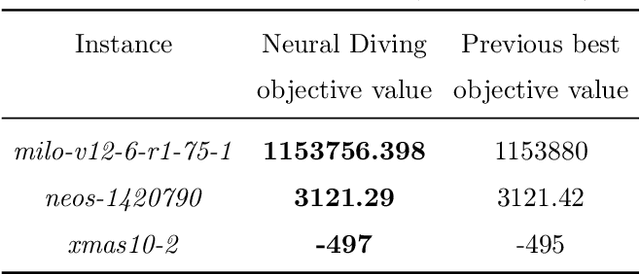
Abstract:Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.
Unsupervised Community Detection with Modularity-Based Attention Model
May 20, 2019
Abstract:In this paper we take a problem of unsupervised nodes clustering on graphs and show how recent advances in attention models can be applied successfully in a "hard" regime of the problem. We propose an unsupervised algorithm that encodes Bethe Hessian embeddings by optimizing soft modularity loss and argue that our model is competitive to both classical and Graph Neural Network (GNN) models while it can be trained on a single graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge