Felix Gimeno
Solving MaxSAT with Matrix Multiplication
Nov 01, 2023
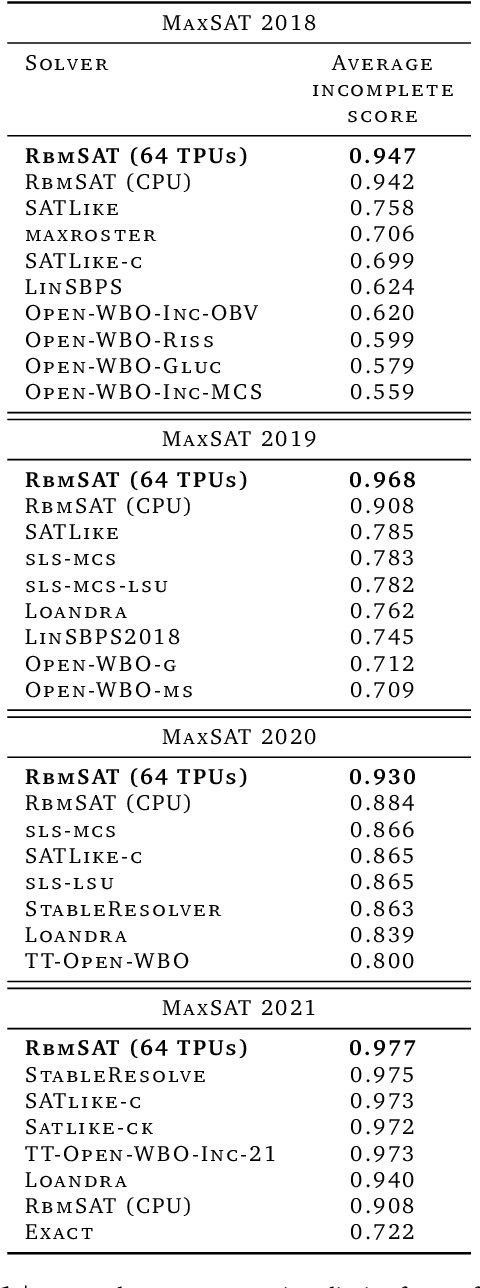


Abstract:We propose an incomplete algorithm for Maximum Satisfiability (MaxSAT) specifically designed to run on neural network accelerators such as GPUs and TPUs. Given a MaxSAT problem instance in conjunctive normal form, our procedure constructs a Restricted Boltzmann Machine (RBM) with an equilibrium distribution wherein the probability of a Boolean assignment is exponential in the number of clauses it satisfies. Block Gibbs sampling is used to stochastically search the space of assignments with parallel Markov chains. Since matrix multiplication is the main computational primitive for block Gibbs sampling in an RBM, our approach leads to an elegantly simple algorithm (40 lines of JAX) well-suited for neural network accelerators. Theoretical results about RBMs guarantee that the required number of visible and hidden units of the RBM scale only linearly with the number of variables and constant-sized clauses in the MaxSAT instance, ensuring that the computational cost of a Gibbs step scales reasonably with the instance size. Search throughput can be increased by batching parallel chains within a single accelerator as well as by distributing them across multiple accelerators. As a further enhancement, a heuristic based on unit propagation running on CPU is periodically applied to the sampled assignments. Our approach, which we term RbmSAT, is a new design point in the algorithm-hardware co-design space for MaxSAT. We present timed results on a subset of problem instances from the annual MaxSAT Evaluation's Incomplete Unweighted Track for the years 2018 to 2021. When allotted the same running time and CPU compute budget (but no TPUs), RbmSAT outperforms other participating solvers on problems drawn from three out of the four years' competitions. Given the same running time on a TPU cluster for which RbmSAT is uniquely designed, it outperforms all solvers on problems drawn from all four years.
Perceiver: General Perception with Iterative Attention
Mar 04, 2021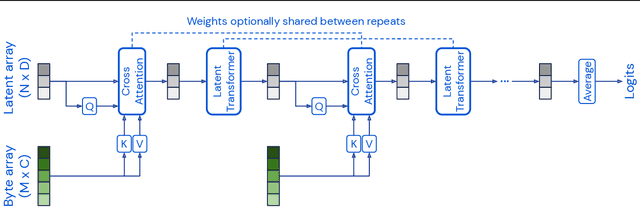

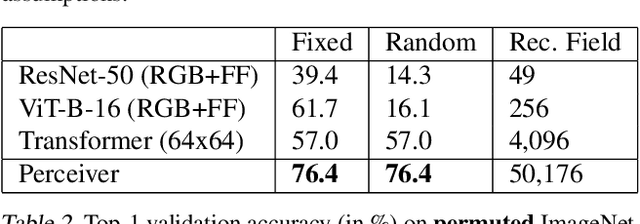
Abstract:Biological systems understand the world by simultaneously processing high-dimensional inputs from modalities as diverse as vision, audition, touch, proprioception, etc. The perception models used in deep learning on the other hand are designed for individual modalities, often relying on domain-specific assumptions such as the local grid structures exploited by virtually all existing vision models. These priors introduce helpful inductive biases, but also lock models to individual modalities. In this paper we introduce the Perceiver - a model that builds upon Transformers and hence makes few architectural assumptions about the relationship between its inputs, but that also scales to hundreds of thousands of inputs, like ConvNets. The model leverages an asymmetric attention mechanism to iteratively distill inputs into a tight latent bottleneck, allowing it to scale to handle very large inputs. We show that this architecture performs competitively or beyond strong, specialized models on classification tasks across various modalities: images, point clouds, audio, video and video+audio. The Perceiver obtains performance comparable to ResNet-50 on ImageNet without convolutions and by directly attending to 50,000 pixels. It also surpasses state-of-the-art results for all modalities in AudioSet.
Solving Mixed Integer Programs Using Neural Networks
Dec 23, 2020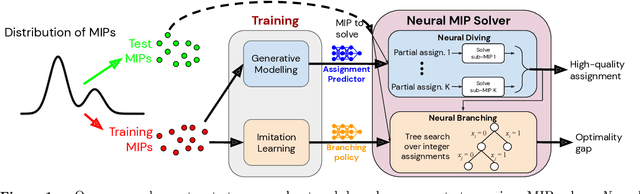
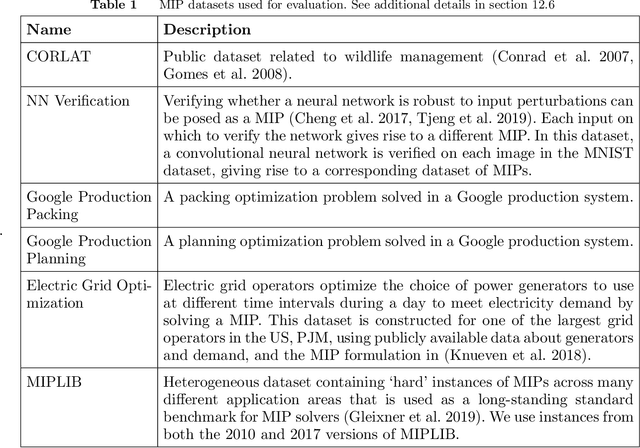
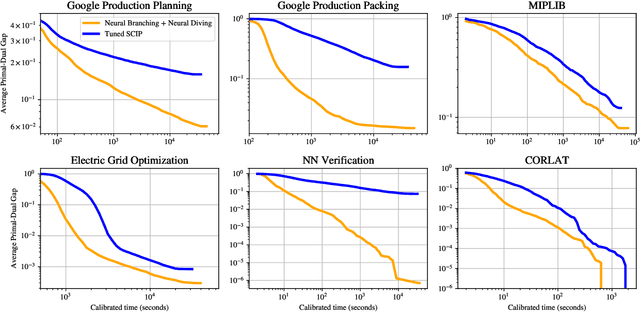
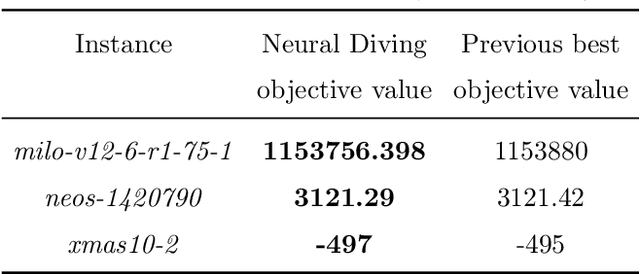
Abstract:Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.
Strong Generalization and Efficiency in Neural Programs
Jul 08, 2020



Abstract:We study the problem of learning efficient algorithms that strongly generalize in the framework of neural program induction. By carefully designing the input / output interfaces of the neural model and through imitation, we are able to learn models that produce correct results for arbitrary input sizes, achieving strong generalization. Moreover, by using reinforcement learning, we optimize for program efficiency metrics, and discover new algorithms that surpass the teacher used in imitation. With this, our approach can learn to outperform custom-written solutions for a variety of problems, as we tested it on sorting, searching in ordered lists and the NP-complete 0/1 knapsack problem, which sets a notable milestone in the field of Neural Program Induction. As highlights, our learned model can perform sorting perfectly on any input data size we tested on, with $O(n log n)$ complexity, whilst outperforming hand-coded algorithms, including quick sort, in number of operations even for list sizes far beyond those seen during training.
Prioritized Unit Propagation with Periodic Resetting is (Almost) All You Need for Random SAT Solving
Dec 04, 2019
Abstract:We propose prioritized unit propagation with periodic resetting, which is a simple but surprisingly effective algorithm for solving random SAT instances that are meant to be hard. In particular, an evaluation on the Random Track of the 2017 and 2018 SAT competitions shows that a basic prototype of this simple idea already ranks at second place in both years. We share this observation in the hope that it helps the SAT community better understand the hardness of random instances used in competitions and inspire other interesting ideas on SAT solving.
REGAL: Transfer Learning For Fast Optimization of Computation Graphs
May 30, 2019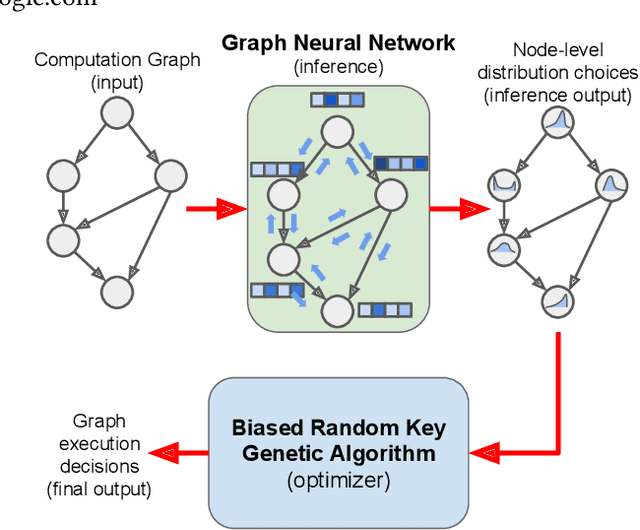
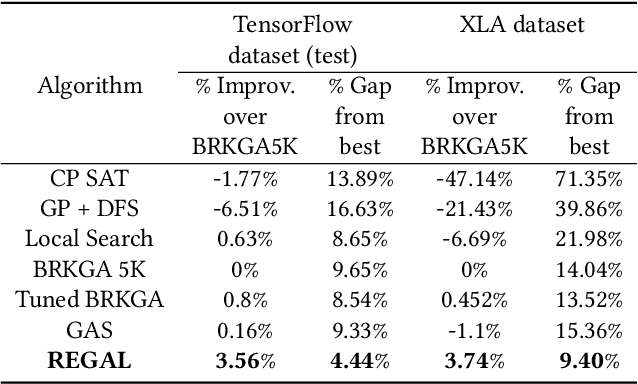
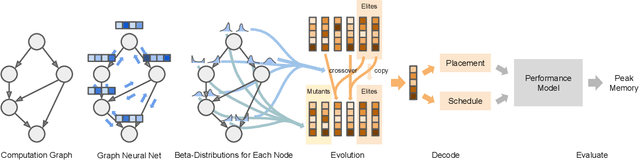
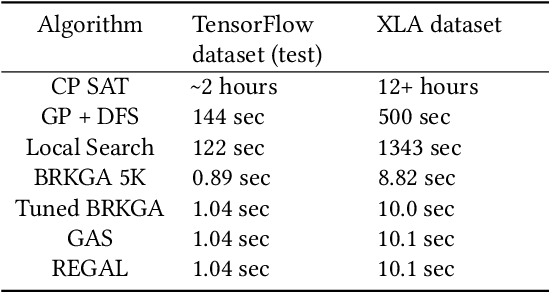
Abstract:We present a deep reinforcement learning approach to optimizing the execution cost of computation graphs in a static compiler. The key idea is to combine a neural network policy with a genetic algorithm, the Biased Random-Key Genetic Algorithm (BRKGA). The policy is trained to predict, given an input graph to be optimized, the node-level probability distributions for sampling mutations and crossovers in BRKGA. Our approach, "REINFORCE-based Genetic Algorithm Learning" (REGAL), uses the policy's ability to transfer to new graphs to significantly improve the solution quality of the genetic algorithm for the same objective evaluation budget. As a concrete application, we show results for minimizing peak memory in TensorFlow graphs by jointly optimizing device placement and scheduling. REGAL achieves on average 3.56% lower peak memory than BRKGA on previously unseen graphs, outperforming all the algorithms we compare to, and giving 4.4x bigger improvement than the next best algorithm. We also evaluate REGAL on a production compiler team's performance benchmark of XLA graphs and achieve on average 3.74% lower peak memory than BRKGA, again outperforming all others. Our approach and analysis is made possible by collecting a dataset of 372 unique real-world TensorFlow graphs, more than an order of magnitude more data than previous work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge