Personalized incentives as feedback design in generalized Nash equilibrium problems
Paper and Code
Mar 24, 2022
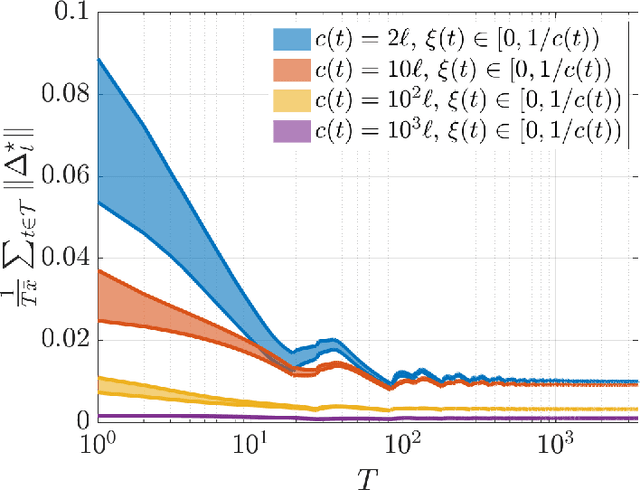
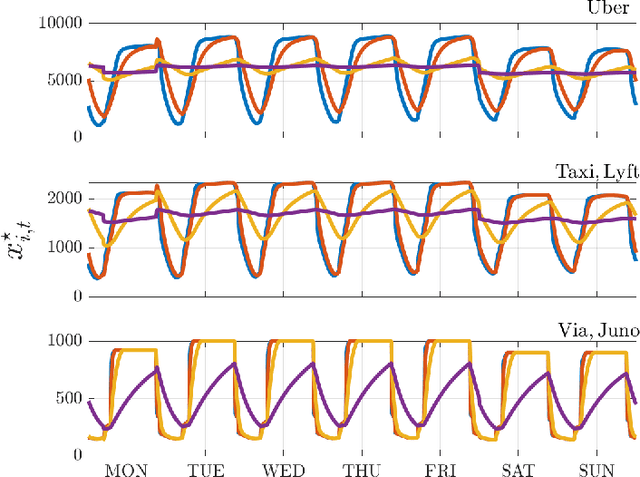
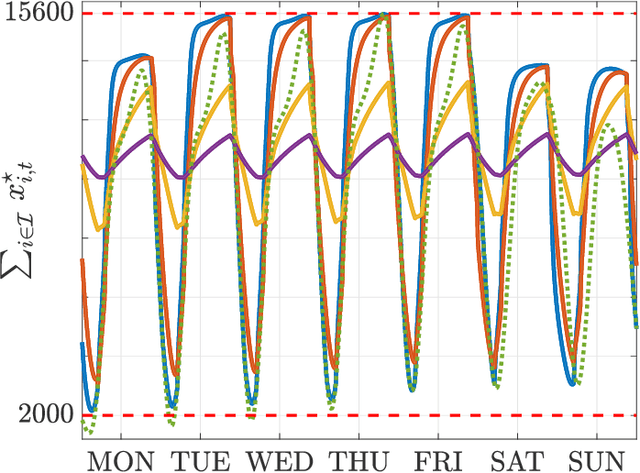
We investigate both stationary and time-varying, nonmonotone generalized Nash equilibrium problems that exhibit symmetric interactions among the agents, which are known to be potential. As may happen in practical cases, however, we envision a scenario in which the formal expression of the underlying potential function is not available, and we design a semi-decentralized Nash equilibrium seeking algorithm. In the proposed two-layer scheme, a coordinator iteratively integrates the (possibly noisy and sporadic) agents' feedback to learn the pseudo-gradients of the agents, and then design personalized incentives for them. On their side, the agents receive those personalized incentives, compute a solution to an extended game, and then return feedback measurements to the coordinator. In the stationary setting, our algorithm returns a Nash equilibrium in case the coordinator is endowed with standard learning policies, while it returns a Nash equilibrium up to a constant, yet adjustable, error in the time-varying case. As a motivating application, we consider the ridehailing service provided by several companies with mobility as a service orchestration, necessary to both handle competition among firms and avoid traffic congestion, which is also adopted to run numerical experiments verifying our results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge