MAPL: Model Agnostic Peer-to-peer Learning

Effective collaboration among heterogeneous clients in a decentralized setting is a rather unexplored avenue in the literature. To structurally address this, we introduce Model Agnostic Peer-to-peer Learning (coined as MAPL) a novel approach to simultaneously learn heterogeneous personalized models as well as a collaboration graph through peer-to-peer communication among neighboring clients. MAPL is comprised of two main modules: (i) local-level Personalized Model Learning (PML), leveraging a combination of intra- and inter-client contrastive losses; (ii) network-wide decentralized Collaborative Graph Learning (CGL) dynamically refining collaboration weights in a privacy-preserving manner based on local task similarities. Our extensive experimentation demonstrates the efficacy of MAPL and its competitive (or, in most cases, superior) performance compared to its centralized model-agnostic counterparts, without relying on any central server. Our code is available and can be accessed here: https://github.com/SayakMukherjee/MAPL

Constrained Hierarchical Clustering via Graph Coarsening and Optimal Cuts

Motivated by extracting and summarizing relevant information in short sentence settings, such as satisfaction questionnaires, hotel reviews, and X/Twitter, we study the problem of clustering words in a hierarchical fashion. In particular, we focus on the problem of clustering with horizontal and vertical structural constraints. Horizontal constraints are typically cannot-link and must-link among words, while vertical constraints are precedence constraints among cluster levels. We overcome state-of-the-art bottlenecks by formulating the problem in two steps: first, as a soft-constrained regularized least-squares which guides the result of a sequential graph coarsening algorithm towards the horizontal feasible set. Then, flat clusters are extracted from the resulting hierarchical tree by computing optimal cut heights based on the available constraints. We show that the resulting approach compares very well with respect to existing algorithms and is computationally light.

Achievement and Fragility of Long-term Equitability

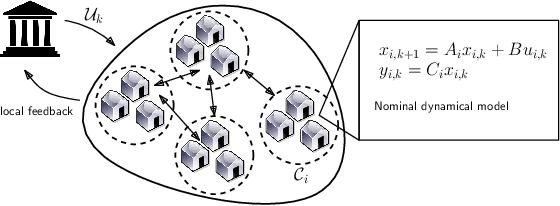
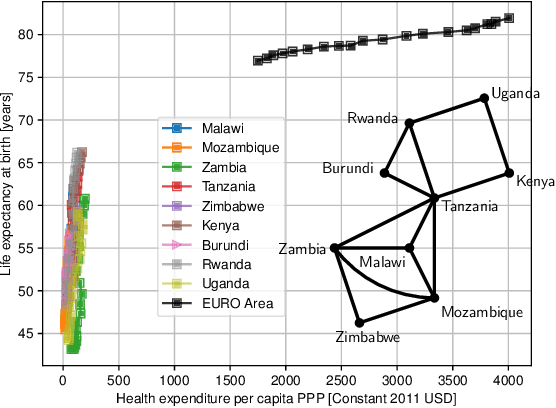
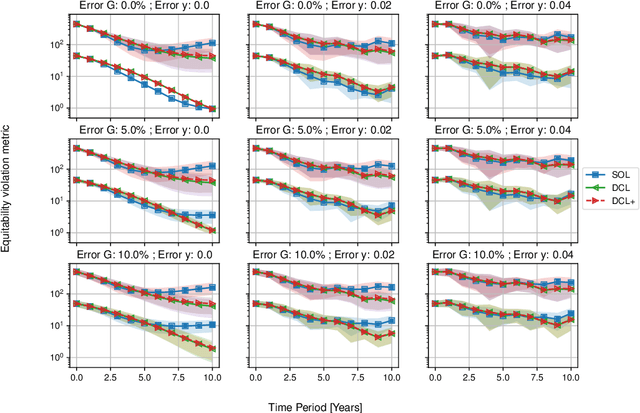
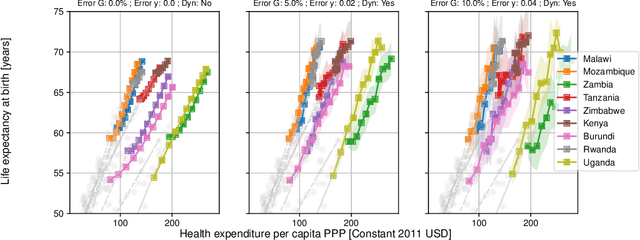
Equipping current decision-making tools with notions of fairness, equitability, or other ethically motivated outcomes, is one of the top priorities in recent research efforts in machine learning, AI, and optimization. In this paper, we investigate how to allocate limited resources to {locally interacting} communities in a way to maximize a pertinent notion of equitability. In particular, we look at the dynamic setting where the allocation is repeated across multiple periods (e.g., yearly), the local communities evolve in the meantime (driven by the provided allocation), and the allocations are modulated by feedback coming from the communities themselves. We employ recent mathematical tools stemming from data-driven feedback online optimization, by which communities can learn their (possibly unknown) evolution, satisfaction, as well as they can share information with the deciding bodies. We design dynamic policies that converge to an allocation that maximize equitability in the long term. We further demonstrate our model and methodology with realistic examples of healthcare and education subsidies design in Sub-Saharian countries. One of the key empirical takeaways from our setting is that long-term equitability is fragile, in the sense that it can be easily lost when deciding bodies weigh in other factors (e.g., equality in allocation) in the allocation strategy. Moreover, a naive compromise, while not providing significant advantage to the communities, can promote inequality in social outcomes.

Personalized incentives as feedback design in generalized Nash equilibrium problems

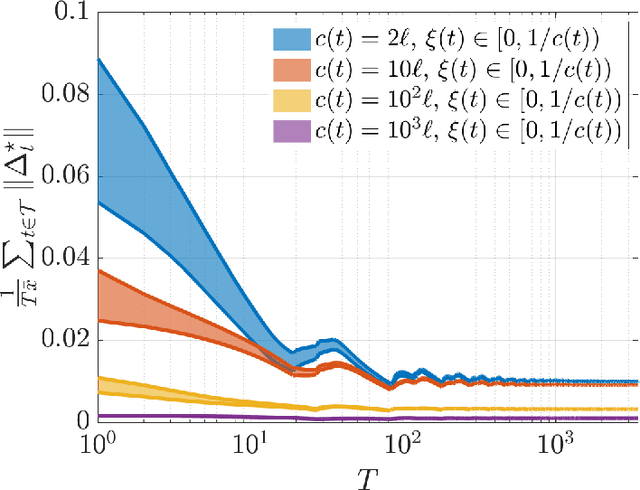
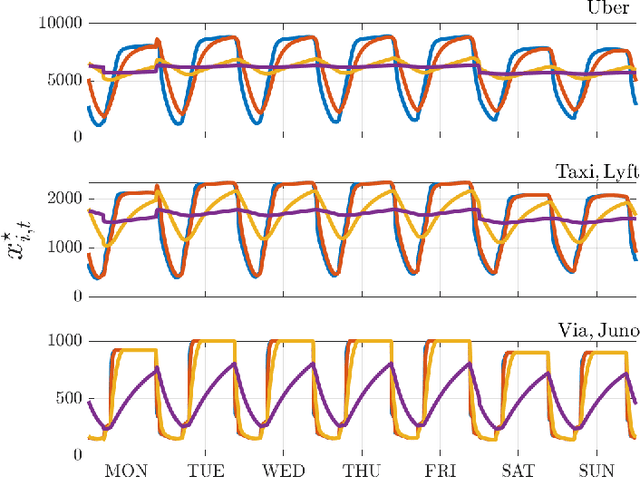
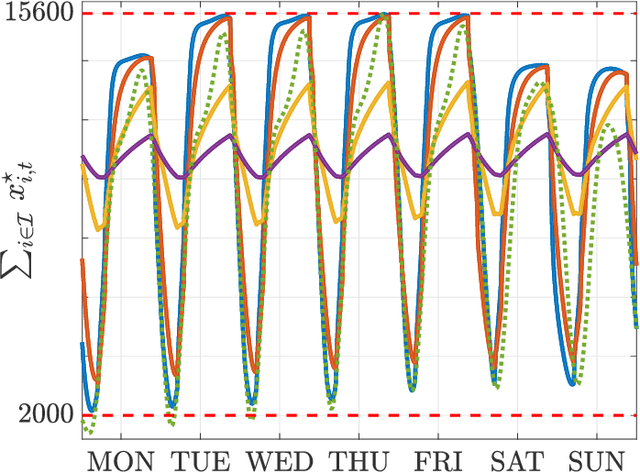
We investigate both stationary and time-varying, nonmonotone generalized Nash equilibrium problems that exhibit symmetric interactions among the agents, which are known to be potential. As may happen in practical cases, however, we envision a scenario in which the formal expression of the underlying potential function is not available, and we design a semi-decentralized Nash equilibrium seeking algorithm. In the proposed two-layer scheme, a coordinator iteratively integrates the (possibly noisy and sporadic) agents' feedback to learn the pseudo-gradients of the agents, and then design personalized incentives for them. On their side, the agents receive those personalized incentives, compute a solution to an extended game, and then return feedback measurements to the coordinator. In the stationary setting, our algorithm returns a Nash equilibrium in case the coordinator is endowed with standard learning policies, while it returns a Nash equilibrium up to a constant, yet adjustable, error in the time-varying case. As a motivating application, we consider the ridehailing service provided by several companies with mobility as a service orchestration, necessary to both handle competition among firms and avoid traffic congestion, which is also adopted to run numerical experiments verifying our results.

Learning equilibria with personalized incentives in a class of nonmonotone games

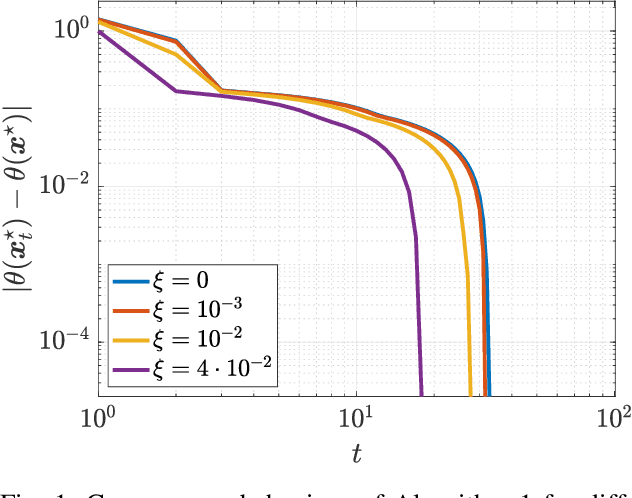
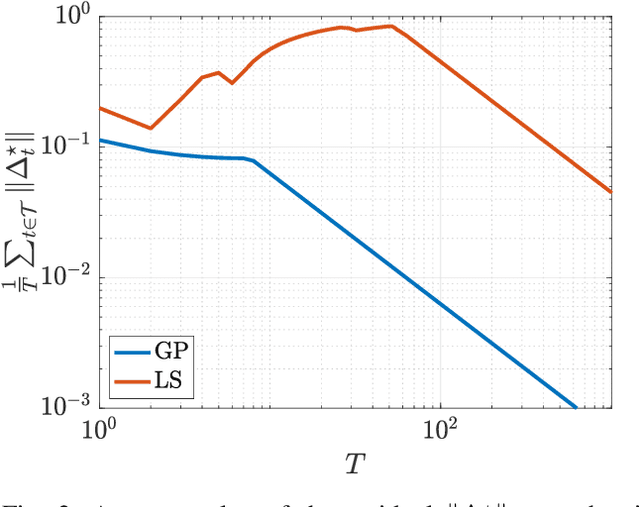
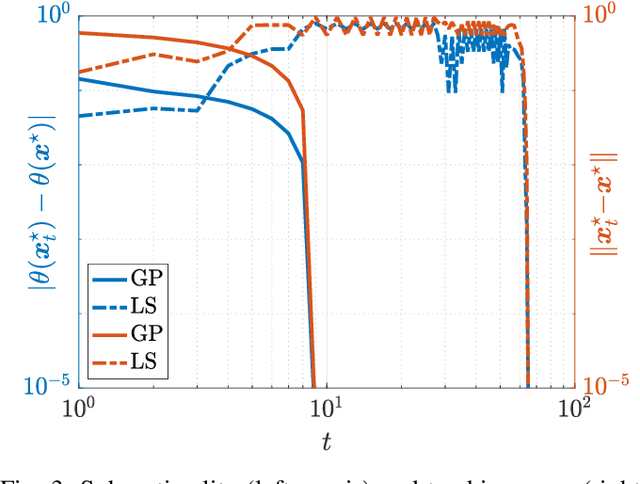
We consider quadratic, nonmonotone generalized Nash equilibrium problems with symmetric interactions among the agents, which are known to be potential. As may happen in practical cases, we envision a scenario in which an explicit expression of the underlying potential function is not available, and we design a two-layer Nash equilibrium seeking algorithm. In the proposed scheme, a coordinator iteratively integrates the noisy agents' feedback to learn the pseudo-gradients of the agents, and then design personalized incentives for them. On their side, the agents receive those personalized incentives, compute a solution to an extended game, and then return feedback measures to the coordinator. We show that our algorithm returns an equilibrium in case the coordinator is endowed with standard learning policies, and corroborate our results on a numerical instance of a hypomonotone game.

OpReg-Boost: Learning to Accelerate Online Algorithms with Operator Regression

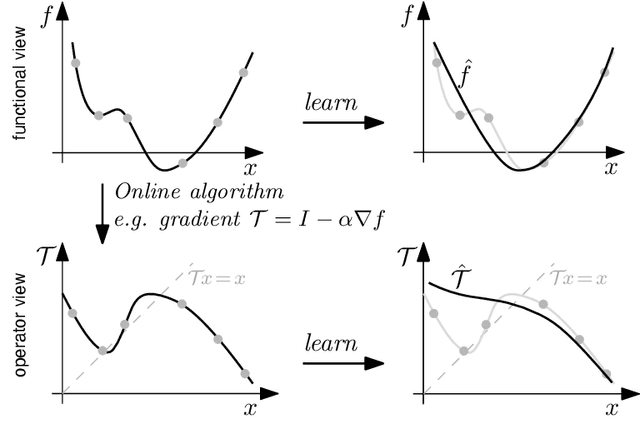
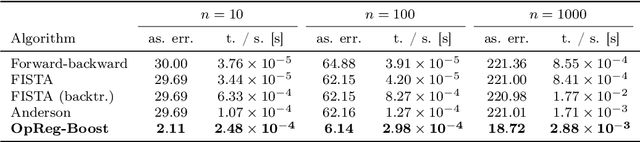
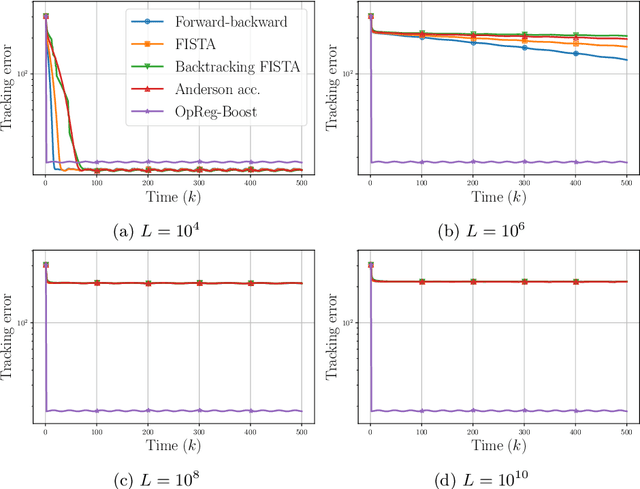
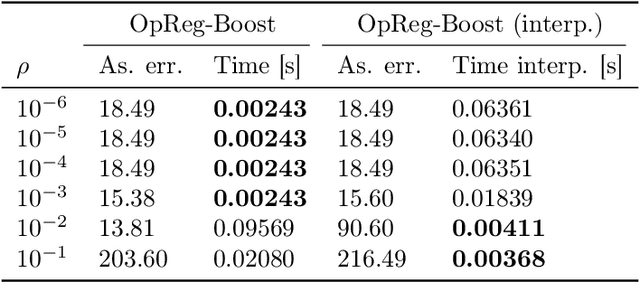
This paper presents a new regularization approach -- termed OpReg-Boost -- to boost the convergence and lessen the asymptotic error of online optimization and learning algorithms. In particular, the paper considers online algorithms for optimization problems with a time-varying (weakly) convex composite cost. For a given online algorithm, OpReg-Boost learns the closest algorithmic map that yields linear convergence; to this end, the learning procedure hinges on the concept of operator regression. We show how to formalize the operator regression problem and propose a computationally-efficient Peaceman-Rachford solver that exploits a closed-form solution of simple quadratically-constrained quadratic programs (QCQPs). Simulation results showcase the superior properties of OpReg-Boost w.r.t. the more classical forward-backward algorithm, FISTA, and Anderson acceleration, and with respect to its close relative convex-regression-boost (CvxReg-Boost) which is also novel but less performing.

Primal and Dual Prediction-Correction Methods for Time-Varying Convex Optimization

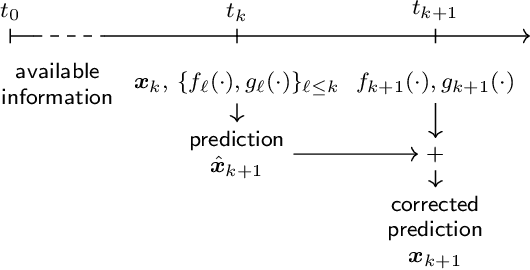
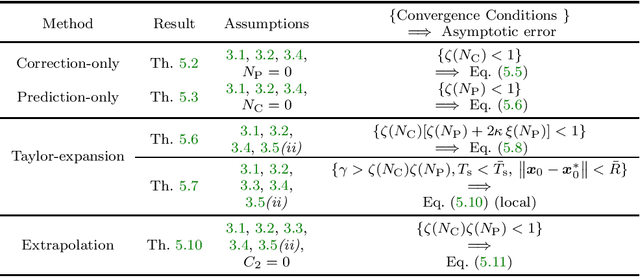
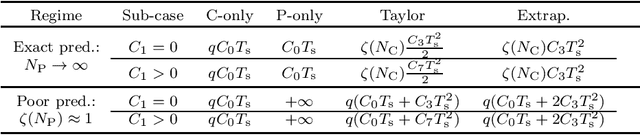
We propose a unified framework for time-varying convex optimization based on the prediction-correction paradigm, both in the primal and dual spaces. In this framework, a continuously varying optimization problem is sampled at fixed intervals, and each problem is approximately solved with a primal or dual correction step. The solution method is warm-started with the output of a prediction step, which solves an approximation of a future problem using past information. Prediction approaches are studied and compared under different sets of assumptions. Examples of algorithms covered by this framework are time-varying versions of the gradient method, splitting methods, and the celebrated alternating direction method of multipliers (ADMM).

Optimization and Learning with Information Streams: Time-varying Algorithms and Applications

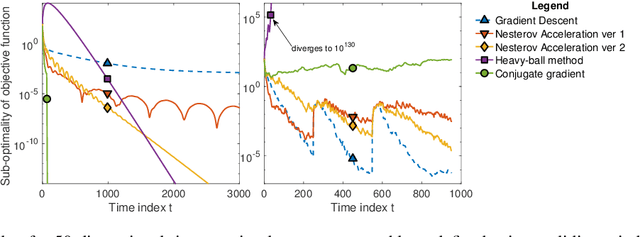
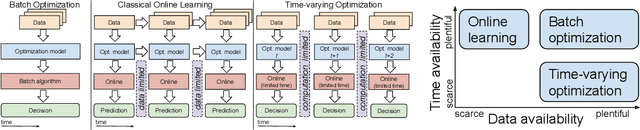
There is a growing cross-disciplinary effort in the broad domain of optimization and learning with streams of data, applied to settings where traditional batch optimization techniques cannot produce solutions at time scales that match the inter-arrival times of the data points due to computational and/or communication bottlenecks. Special types of online algorithms can handle this situation, and this article focuses on such time-varying optimization algorithms, with emphasis on Machine Leaning and Signal Processing, as well as data-driven control. Approaches for the design of time-varying first-order methods are discussed, with emphasis on algorithms that can handle errors in the gradient, as may arise when the gradient is estimated. Insights on performance metrics and accompanying claims are provided, along with evidence of cases where algorithms that are provably convergent in batch optimization perform poorly in an online regime. The role of distributed computation is discussed. Illustrative numerical examples for a number of applications of broad interest are provided to convey key ideas.

Inexact Online Proximal-gradient Method for Time-varying Convex Optimization

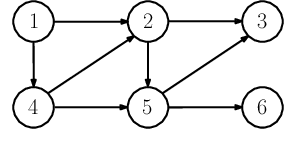
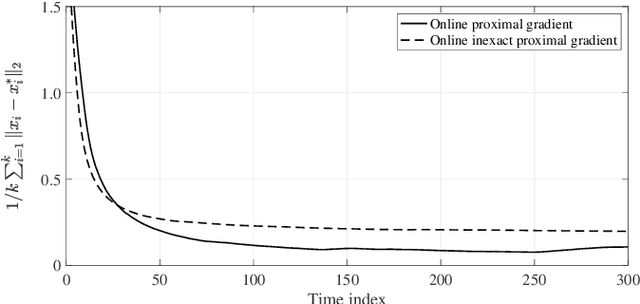
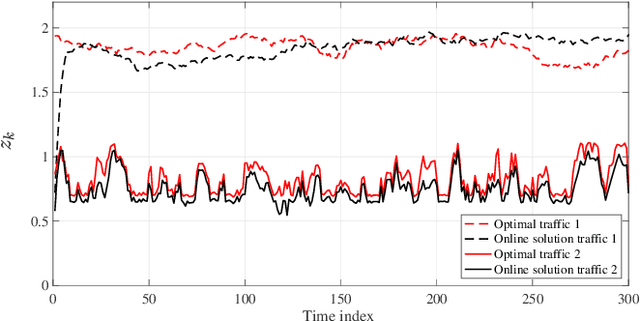
This paper considers an online proximal-gradient method to track the minimizers of a composite convex function that may continuously evolve over time. The online proximal-gradient method is inexact, in the sense that: (i) it relies on an approximate first-order information of the smooth component of the cost; and, (ii) the proximal operator (with respect to the non-smooth term) may be computed only up to a certain precision. Under suitable assumptions, convergence of the error iterates is established for strongly convex cost functions. On the other hand, the dynamic regret is investigated when the cost is not strongly convex, under the additional assumption that the problem includes feasibility sets that are compact. Bounds are expressed in terms of the cumulative error and the path length of the optimal solutions. This suggests how to allocate resources to strike a balance between performance and precision in the gradient computation and in the proximal operator.

Pursuit of Low-Rank Models of Time-Varying Matrices Robust to Sparse and Measurement Noise

In tracking of time-varying low-rank models of time-varying matrices, we present a method robust to both uniformly-distributed measurement noise and arbitrarily-distributed "sparse" noise. In theory, we bound the tracking error. In practice, our use of randomised coordinate descent is scalable and allows for encouraging results on changedetection.net, a benchmark.