OpReg-Boost: Learning to Accelerate Online Algorithms with Operator Regression
Paper and Code
May 27, 2021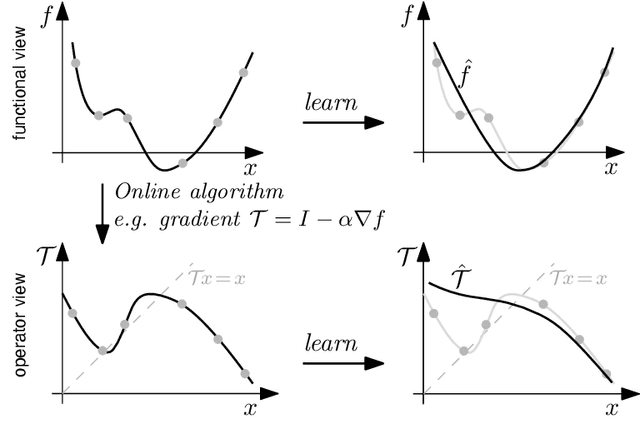
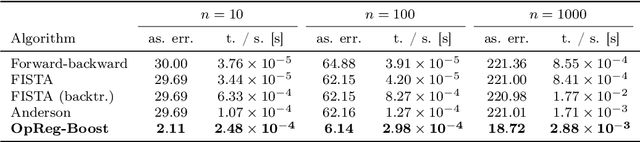
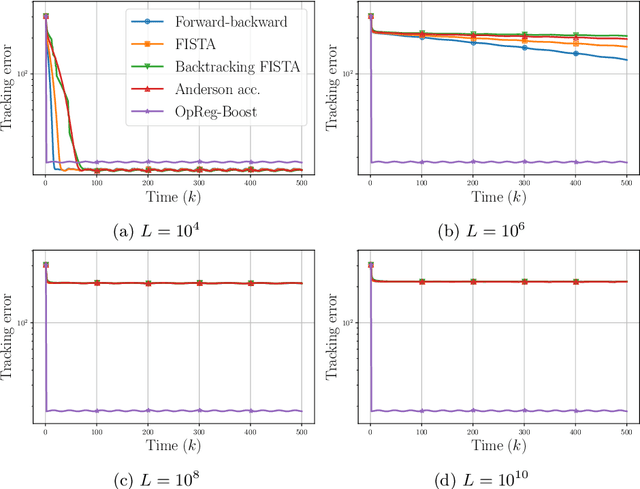
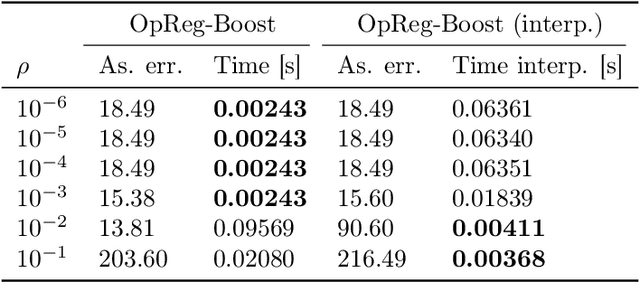
This paper presents a new regularization approach -- termed OpReg-Boost -- to boost the convergence and lessen the asymptotic error of online optimization and learning algorithms. In particular, the paper considers online algorithms for optimization problems with a time-varying (weakly) convex composite cost. For a given online algorithm, OpReg-Boost learns the closest algorithmic map that yields linear convergence; to this end, the learning procedure hinges on the concept of operator regression. We show how to formalize the operator regression problem and propose a computationally-efficient Peaceman-Rachford solver that exploits a closed-form solution of simple quadratically-constrained quadratic programs (QCQPs). Simulation results showcase the superior properties of OpReg-Boost w.r.t. the more classical forward-backward algorithm, FISTA, and Anderson acceleration, and with respect to its close relative convex-regression-boost (CvxReg-Boost) which is also novel but less performing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge