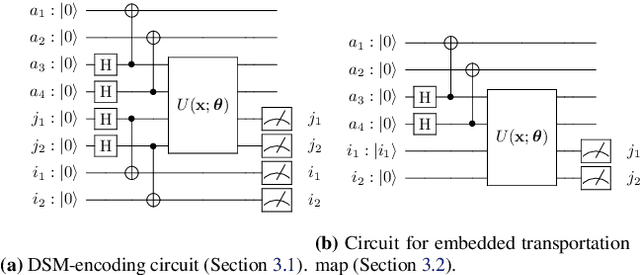
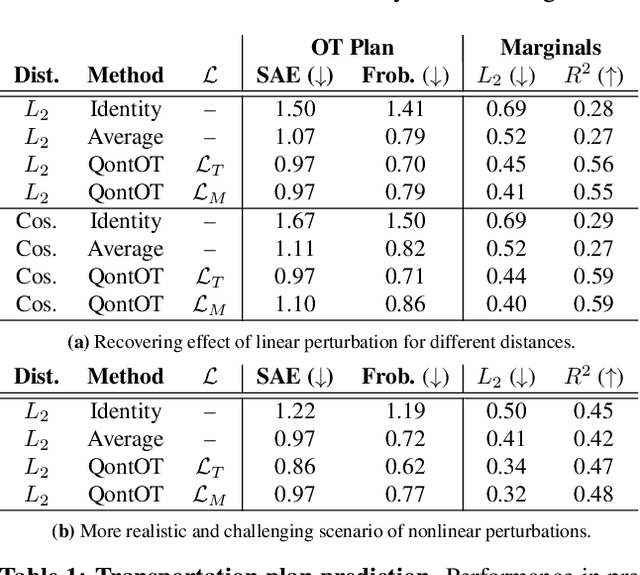
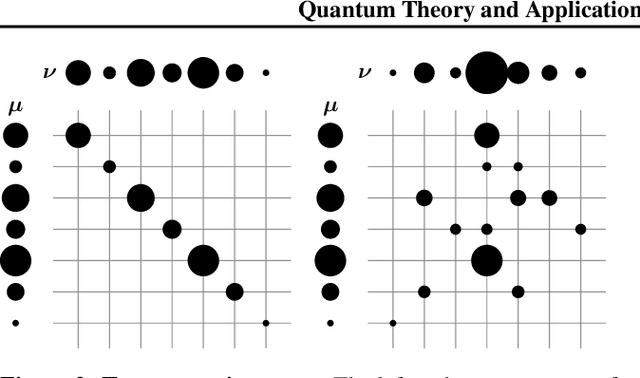
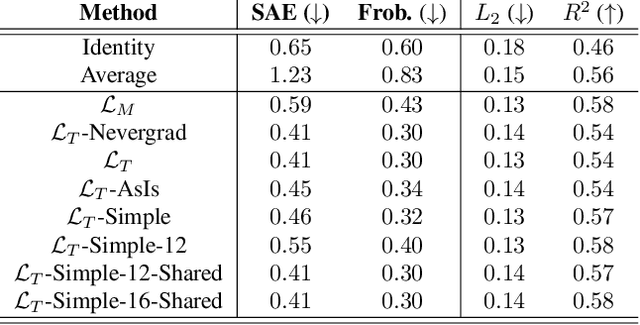
Quantum Theory and Application of Contextual Optimal Transport

Optimal Transport (OT) has fueled machine learning (ML) applications across many domains. In cases where paired data measurements ($\mu$, $\nu$) are coupled to a context variable $p_i$ , one may aspire to learn a global transportation map that can be parameterized through a potentially unseen con-text. Existing approaches utilize Neural OT and largely rely on Brenier's theorem. Here, we propose a first-of-its-kind quantum computing formulation for amortized optimization of contextualized transportation plans. We exploit a direct link between doubly stochastic matrices and unitary operators thus finding a natural connection between OT and quantum computation. We verify our method on synthetic and real data, by predicting variations in cell type distributions parameterized through drug dosage as context. Our comparisons to several baselines reveal that our method can capture dose-induced variations in cell distributions, even to some extent when dosages are extrapolated and sometimes with performance similar to the best classical models. In summary, this is a first step toward learning to predict contextualized transportation plans through quantum.

Deep Autoencoders with Value-at-Risk Thresholding for Unsupervised Anomaly Detection

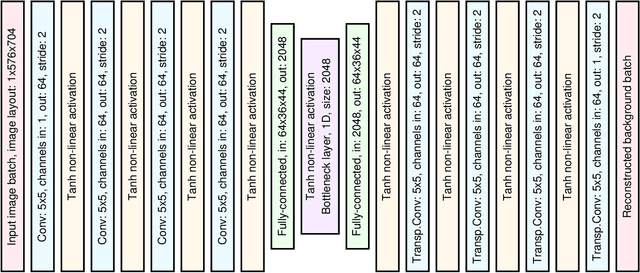
Many real-world monitoring and surveillance applications require non-trivial anomaly detection to be run in the streaming model. We consider an incremental-learning approach, wherein a deep-autoencoding (DAE) model of what is normal is trained and used to detect anomalies at the same time. In the detection of anomalies, we utilise a novel thresholding mechanism, based on value at risk (VaR). We compare the resulting convolutional neural network (CNN) against a number of subspace methods, and present results on changedetection net.

Pursuit of Low-Rank Models of Time-Varying Matrices Robust to Sparse and Measurement Noise

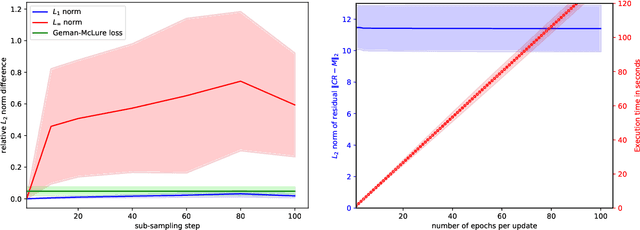
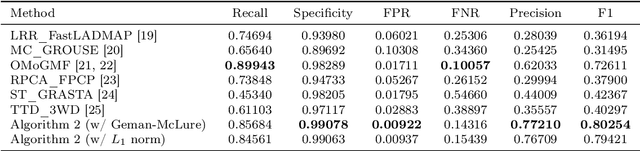
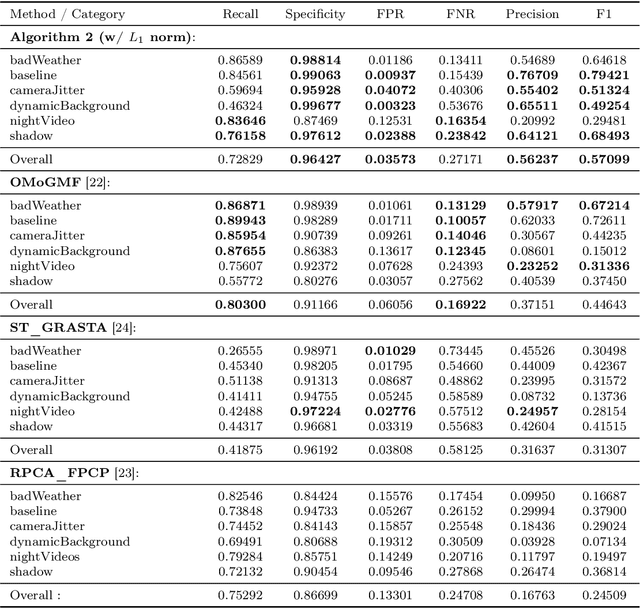
In tracking of time-varying low-rank models of time-varying matrices, we present a method robust to both uniformly-distributed measurement noise and arbitrarily-distributed "sparse" noise. In theory, we bound the tracking error. In practice, our use of randomised coordinate descent is scalable and allows for encouraging results on changedetection.net, a benchmark.

Where computer vision can aid physics: dynamic cloud motion forecasting from satellite images

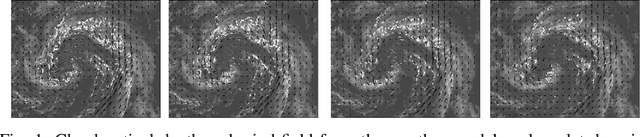
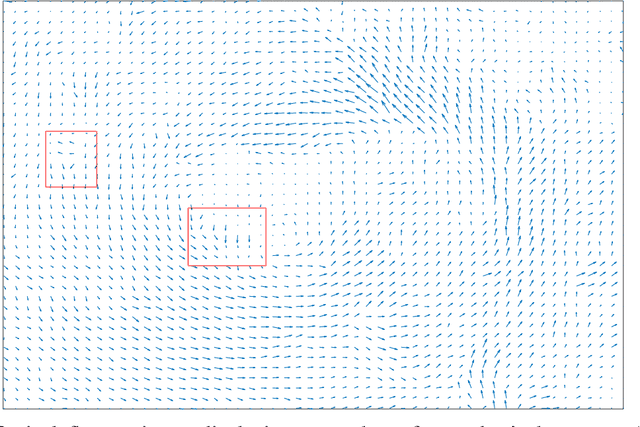
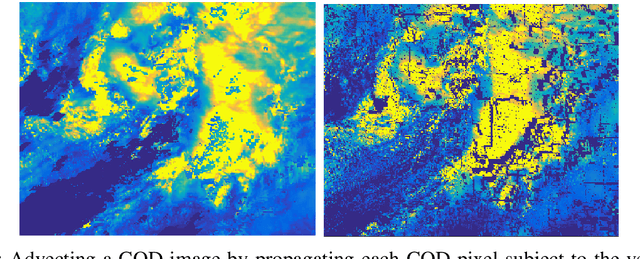
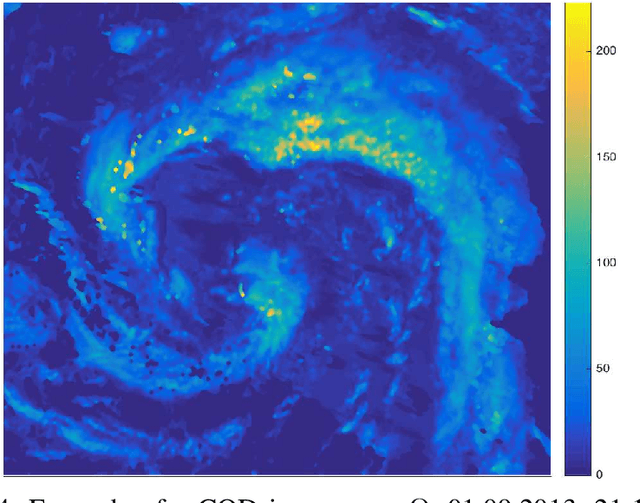
This paper describes a new algorithm for solar energy forecasting from a sequence of Cloud Optical Depth (COD) images. The algorithm is based on the following simple observation: the dynamics of clouds represented by COD images resembles the motion (transport) of a density in a fluid flow. This suggests that, to forecast the motion of COD images, it is sufficient to forecast the flow. The latter, in turn, can be accomplished by fitting a parametric model of the fluid flow to the COD images observed in the past. Namely, the learning phase of the algorithm is composed of the following steps: (i) given a sequence of COD images, the snapshots of the optical flow are estimated from two consecutive COD images; (ii) these snapshots are then assimilated into a Navier-Stokes Equation (NSE), i.e. an initial velocity field for NSE is selected so that the corresponding NSE' solution is as close as possible to the optical flow snapshots. The prediction phase consists of utilizing a linear transport equation, which describes the propagation of COD images in the fluid flow predicted by NSE, to estimate the future motion of the COD images. The algorithm has been tested on COD images provided by two geostationary operational environmental satellites from NOAA serving the west-hemisphere.