Learning equilibria with personalized incentives in a class of nonmonotone games
Paper and Code
Nov 06, 2021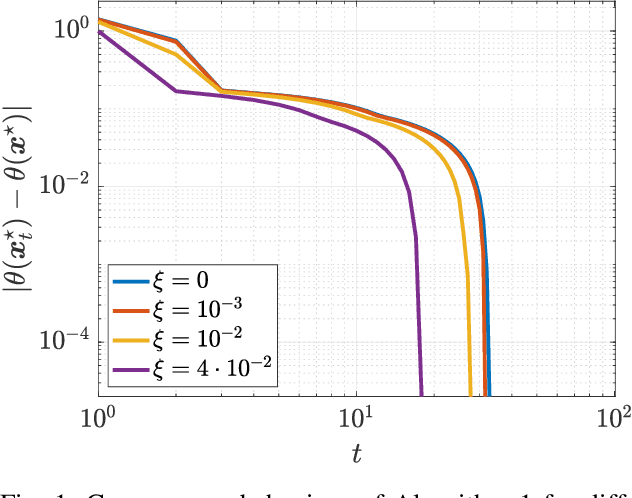
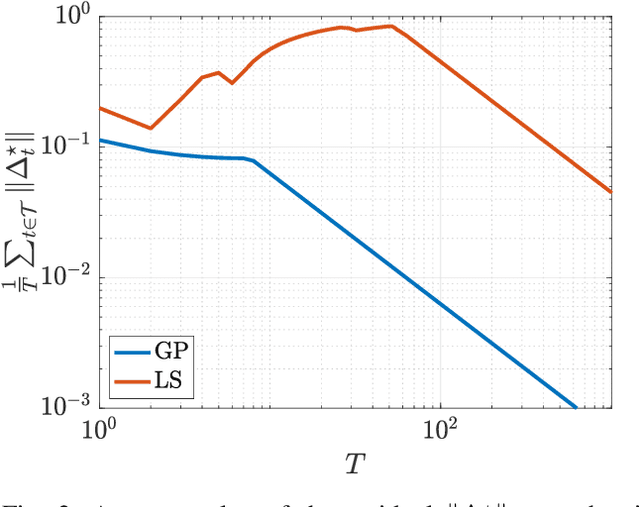
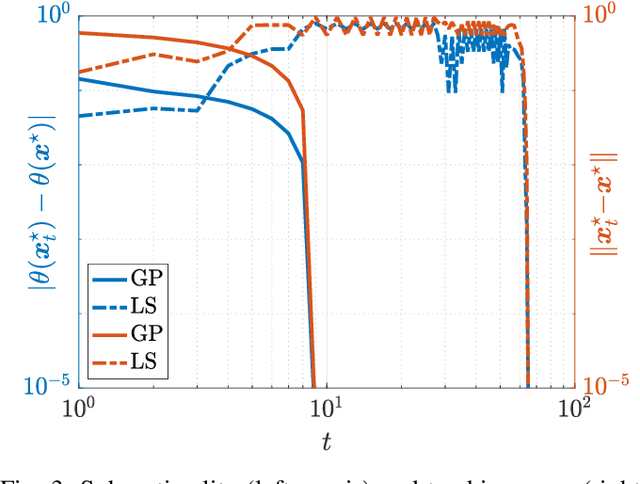

We consider quadratic, nonmonotone generalized Nash equilibrium problems with symmetric interactions among the agents, which are known to be potential. As may happen in practical cases, we envision a scenario in which an explicit expression of the underlying potential function is not available, and we design a two-layer Nash equilibrium seeking algorithm. In the proposed scheme, a coordinator iteratively integrates the noisy agents' feedback to learn the pseudo-gradients of the agents, and then design personalized incentives for them. On their side, the agents receive those personalized incentives, compute a solution to an extended game, and then return feedback measures to the coordinator. We show that our algorithm returns an equilibrium in case the coordinator is endowed with standard learning policies, and corroborate our results on a numerical instance of a hypomonotone game.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge