Model order reduction of deep structured state-space models: A system-theoretic approach

With a specific emphasis on control design objectives, achieving accurate system modeling with limited complexity is crucial in parametric system identification. The recently introduced deep structured state-space models (SSM), which feature linear dynamical blocks as key constituent components, offer high predictive performance. However, the learned representations often suffer from excessively large model orders, which render them unsuitable for control design purposes. The current paper addresses this challenge by means of system-theoretic model order reduction techniques that target the linear dynamical blocks of SSMs. We introduce two regularization terms which can be incorporated into the training loss for improved model order reduction. In particular, we consider modal $\ell_1$ and Hankel nuclear norm regularization to promote sparsity, allowing one to retain only the relevant states without sacrificing accuracy. The presented regularizers lead to advantages in terms of parsimonious representations and faster inference resulting from the reduced order models. The effectiveness of the proposed methodology is demonstrated using real-world ground vibration data from an aircraft.

Synthetic data generation for system identification: leveraging knowledge transfer from similar systems

This paper addresses the challenge of overfitting in the learning of dynamical systems by introducing a novel approach for the generation of synthetic data, aimed at enhancing model generalization and robustness in scenarios characterized by data scarcity. Central to the proposed methodology is the concept of knowledge transfer from systems within the same class. Specifically, synthetic data is generated through a pre-trained meta-model that describes a broad class of systems to which the system of interest is assumed to belong. Training data serves a dual purpose: firstly, as input to the pre-trained meta model to discern the system's dynamics, enabling the prediction of its behavior and thereby generating synthetic output sequences for new input sequences; secondly, in conjunction with synthetic data, to define the loss function used for model estimation. A validation dataset is used to tune a scalar hyper-parameter balancing the relative importance of training and synthetic data in the definition of the loss function. The same validation set can be also used for other purposes, such as early stopping during the training, fundamental to avoid overfitting in case of small-size training datasets. The efficacy of the approach is shown through a numerical example that highlights the advantages of integrating synthetic data into the system identification process.

Shedding Light on the Ageing of Extra Virgin Olive Oil: Probing the Impact of Temperature with Fluorescence Spectroscopy and Machine Learning Techniques

This work systematically investigates the oxidation of extra virgin olive oil (EVOO) under accelerated storage conditions with UV absorption and total fluorescence spectroscopy. With the large amount of data collected, it proposes a method to monitor the oil's quality based on machine learning applied to highly-aggregated data. EVOO is a high-quality vegetable oil that has earned worldwide reputation for its numerous health benefits and excellent taste. Despite its outstanding quality, EVOO degrades over time owing to oxidation, which can affect both its health qualities and flavour. Therefore, it is highly relevant to quantify the effects of oxidation on EVOO and develop methods to assess it that can be easily implemented under field conditions, rather than in specialized laboratories. The following study demonstrates that fluorescence spectroscopy has the capability to monitor the effect of oxidation and assess the quality of EVOO, even when the data are highly aggregated. It shows that complex laboratory equipment is not necessary to exploit fluorescence spectroscopy using the proposed method and that cost-effective solutions, which can be used in-field by non-scientists, could provide an easily-accessible assessment of the quality of EVOO.

Learning neural state-space models: do we need a state estimator?

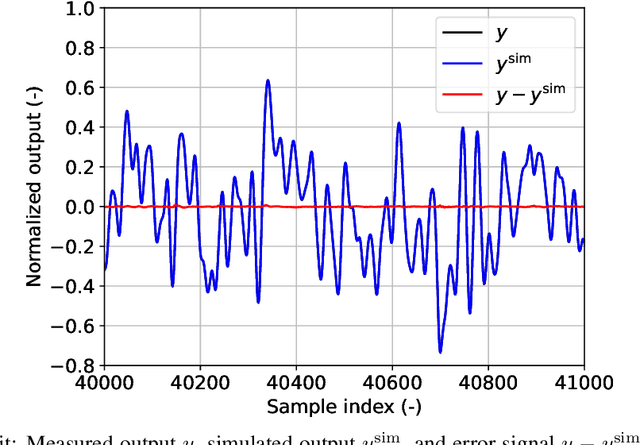
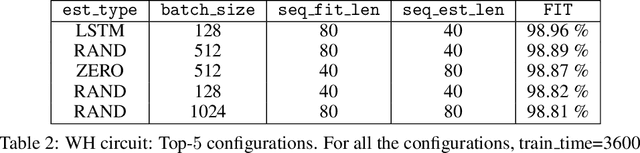
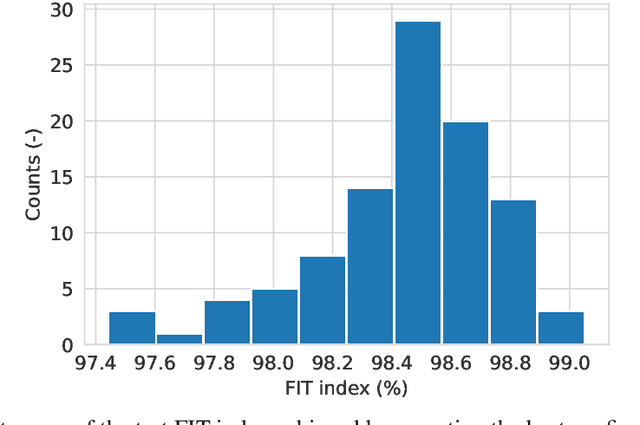
In recent years, several algorithms for system identification with neural state-space models have been introduced. Most of the proposed approaches are aimed at reducing the computational complexity of the learning problem, by splitting the optimization over short sub-sequences extracted from a longer training dataset. Different sequences are then processed simultaneously within a minibatch, taking advantage of modern parallel hardware for deep learning. An issue arising in these methods is the need to assign an initial state for each of the sub-sequences, which is required to run simulations and thus to evaluate the fitting loss. In this paper, we provide insights for calibration of neural state-space training algorithms based on extensive experimentation and analyses performed on two recognized system identification benchmarks. Particular focus is given to the choice and the role of the initial state estimation. We demonstrate that advanced initial state estimation techniques are really required to achieve high performance on certain classes of dynamical systems, while for asymptotically stable ones basic procedures such as zero or random initialization already yield competitive performance.

Deep learning with transfer functions: new applications in system identification

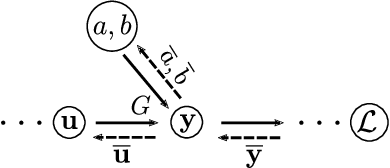
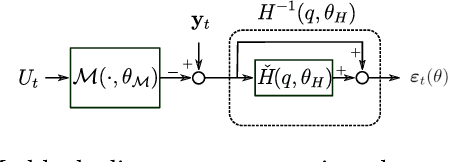
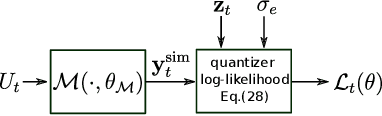
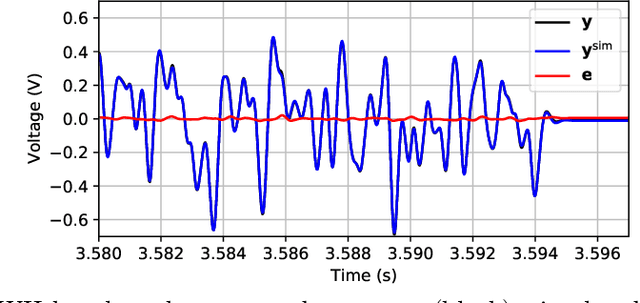
This paper presents a linear dynamical operator described in terms of a rational transfer function, endowed with a well-defined and efficient back-propagation behavior for automatic derivatives computation. The operator enables end-to-end training of structured networks containing linear transfer functions and other differentiable units {by} exploiting standard deep learning software. Two relevant applications of the operator in system identification are presented. The first one consists in the integration of {prediction error methods} in deep learning. The dynamical operator is included as {the} last layer of a neural network in order to obtain the optimal one-step-ahead prediction error. The second one considers identification of general block-oriented models from quantized data. These block-oriented models are constructed by combining linear dynamical operators with static nonlinearities described as standard feed-forward neural networks. A custom loss function corresponding to the log-likelihood of quantized output observations is defined. For gradient-based optimization, the derivatives of the log-likelihood are computed by applying the back-propagation algorithm through the whole network. Two system identification benchmarks are used to show the effectiveness of the proposed methodologies.