Learning neural state-space models: do we need a state estimator?
Paper and Code
Jun 26, 2022
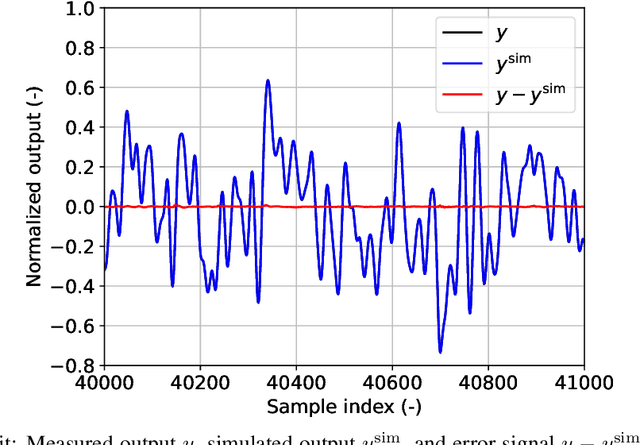
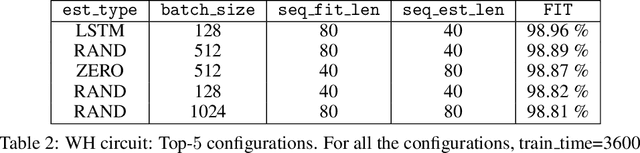
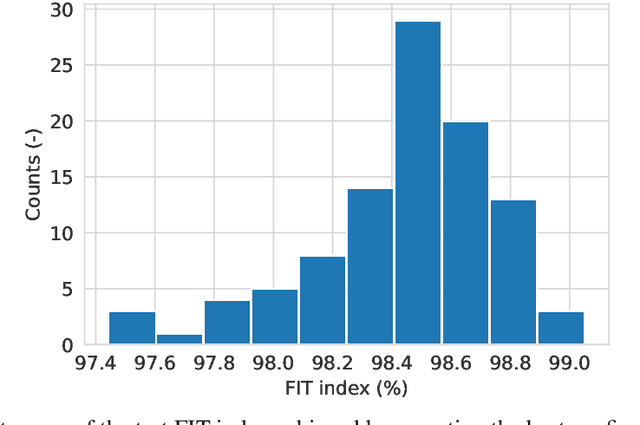
In recent years, several algorithms for system identification with neural state-space models have been introduced. Most of the proposed approaches are aimed at reducing the computational complexity of the learning problem, by splitting the optimization over short sub-sequences extracted from a longer training dataset. Different sequences are then processed simultaneously within a minibatch, taking advantage of modern parallel hardware for deep learning. An issue arising in these methods is the need to assign an initial state for each of the sub-sequences, which is required to run simulations and thus to evaluate the fitting loss. In this paper, we provide insights for calibration of neural state-space training algorithms based on extensive experimentation and analyses performed on two recognized system identification benchmarks. Particular focus is given to the choice and the role of the initial state estimation. We demonstrate that advanced initial state estimation techniques are really required to achieve high performance on certain classes of dynamical systems, while for asymptotically stable ones basic procedures such as zero or random initialization already yield competitive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge