Direct Collocation Methods for Trajectory Optimization in Constrained Robotic Systems

Direct collocation methods are powerful tools to solve trajectory optimization problems in robotics. While their resulting trajectories tend to be dynamically accurate, they may also present large kinematic errors in the case of constrained mechanical systems, i.e., those whose state coordinates are subject to holonomic or nonholonomic constraints, like loop-closure or rolling-contact constraints. These constraints confine the robot trajectories to an implicitly-defined manifold, which complicates the computation of accurate solutions. Discretization errors inherent to the transcription of the problem easily make the trajectories drift away from this manifold, which results in physically inconsistent motions that are difficult to track with a controller. This paper reviews existing methods to deal with this problem and proposes new ones to overcome their limitations. Current approaches either disregard the kinematic constraints (which leads to drift accumulation) or modify the system dynamics to keep the trajectory close to the manifold (which adds artificial forces or energy dissipation to the system). The methods we propose, in contrast, achieve full drift elimination on the discrete trajectory, or even along the continuous one, without artificial modifications of the system dynamics. We illustrate and compare the methods using various examples of different complexity.

A Convolutional Neural Network for the Automatic Diagnosis of Collagen VI related Muscular Dystrophies

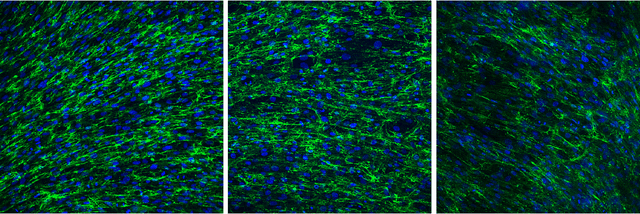
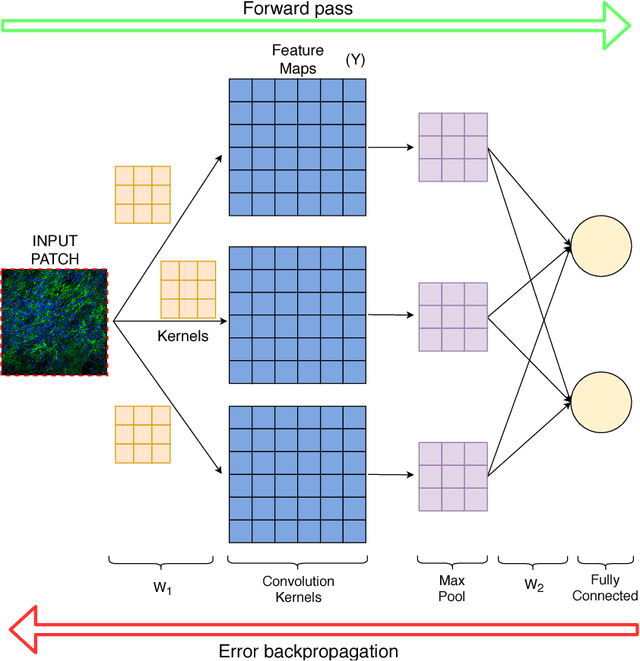
The development of machine learning systems for the diagnosis of rare diseases is challenging mainly due the lack of data to study them. Despite this challenge, this paper proposes a system for the Computer Aided Diagnosis (CAD) of low-prevalence, congenital muscular dystrophies from confocal microscopy images. The proposed CAD system relies on a Convolutional Neural Network (CNN) which performs an independent classification for non-overlapping patches tiling the input image, and generates an overall decision summarizing the individual decisions for the patches on the query image. This decision scheme points to the possibly problematic areas in the input images and provides a global quantitative evaluation of the state of the patients, which is fundamental for diagnosis and to monitor the efficiency of therapies.

Kinodynamic Planning on Constraint Manifolds

This paper presents a motion planner for systems subject to kinematic and dynamic constraints. The former appear when kinematic loops are present in the system, such as in parallel manipulators, in robots that cooperate to achieve a given task, or in situations involving contacts with the environment. The latter are necessary to obtain realistic trajectories, taking into account the forces acting on the system. The kinematic constraints make the state space become an implicitly-defined manifold, which complicates the application of common motion planning techniques. To address this issue, the planner constructs an atlas of the state space manifold incrementally, and uses this atlas both to generate random states and to dynamically simulate the steering of the system towards such states. The resulting tools are then exploited to construct a rapidly-exploring random tree (RRT) over the state space. To the best of our knowledge, this is the first randomized kinodynamic planner for implicitly-defined state spaces. The test cases presented in this paper validate the approach in significantly-complex systems.

Sampling Strategies for Path Planning under Kinematic Constraints

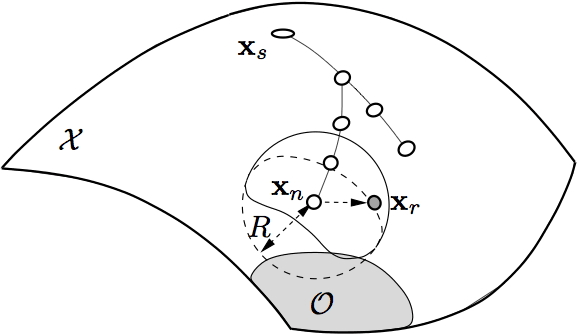
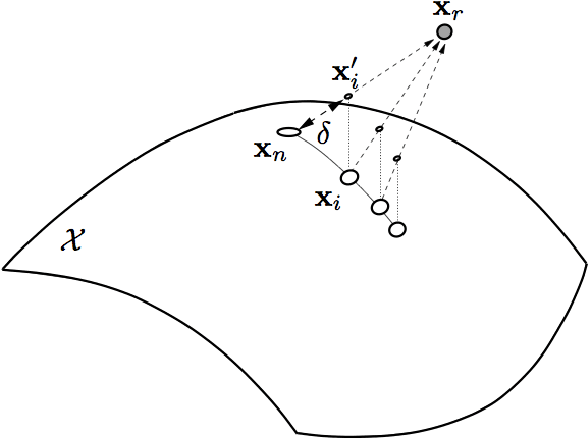
A well-known weakness of the probabilistic path planners is the so-called narrow passage problem, where a region with a relatively low probability of being sampled must be explored to find a solution path. Many strategies have been proposed to alleviate this problem, most of them based on biasing the sampling distribution. When kinematic constraints appear in the problem, the configuration space typically becomes a non-parametrizable, implicit manifold. Unfortunately, this invalidates most of the existing sampling bias approaches, which rely on an explicit parametrization of the space to explore. In this paper, we propose and evaluate three novel strategies to bias the sampling under the presence of narrow passages in kinematically-constrained systems.