Equivariant Deep Learning of Mixed-Integer Optimal Control Solutions for Vehicle Decision Making and Motion Planning

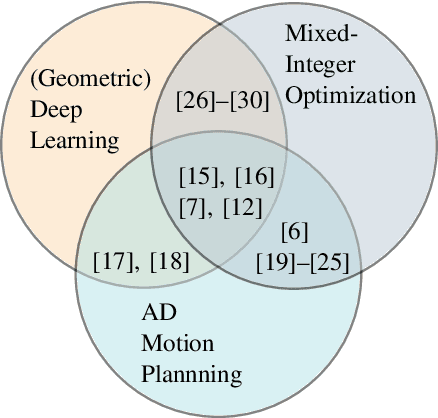
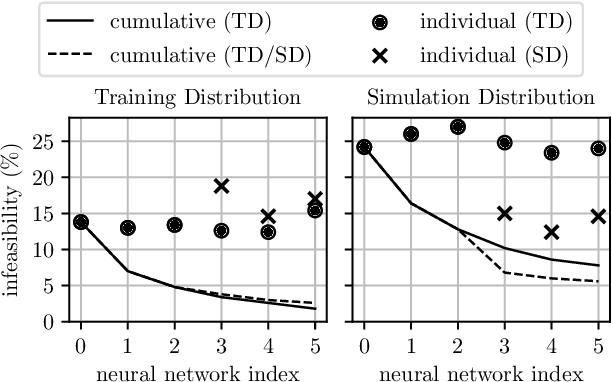
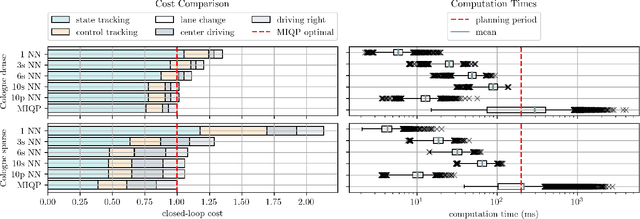
Mixed-integer quadratic programs (MIQPs) are a versatile way of formulating vehicle decision making and motion planning problems, where the prediction model is a hybrid dynamical system that involves both discrete and continuous decision variables. However, even the most advanced MIQP solvers can hardly account for the challenging requirements of automotive embedded platforms. Thus, we use machine learning to simplify and hence speed up optimization. Our work builds on recent ideas for solving MIQPs in real-time by training a neural network to predict the optimal values of integer variables and solving the remaining problem by online quadratic programming. Specifically, we propose a recurrent permutation equivariant deep set that is particularly suited for imitating MIQPs that involve many obstacles, which is often the major source of computational burden in motion planning problems. Our framework comprises also a feasibility projector that corrects infeasible predictions of integer variables and considerably increases the likelihood of computing a collision-free trajectory. We evaluate the performance, safety and real-time feasibility of decision-making for autonomous driving using the proposed approach on realistic multi-lane traffic scenarios with interactive agents in SUMO simulations.

Path Planning and Motion Control for Accurate Positioning of Car-like Robots

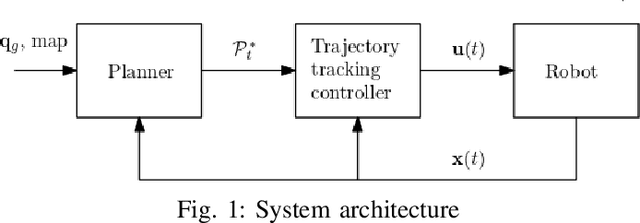
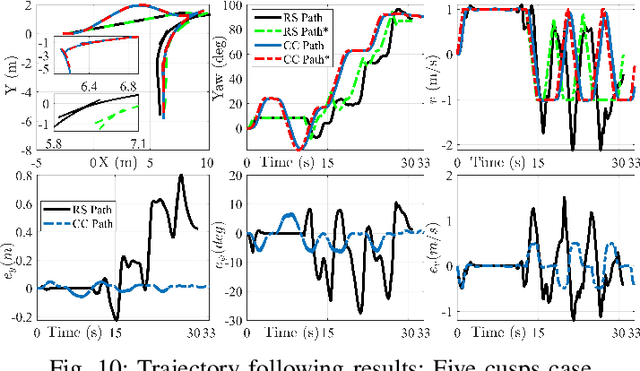
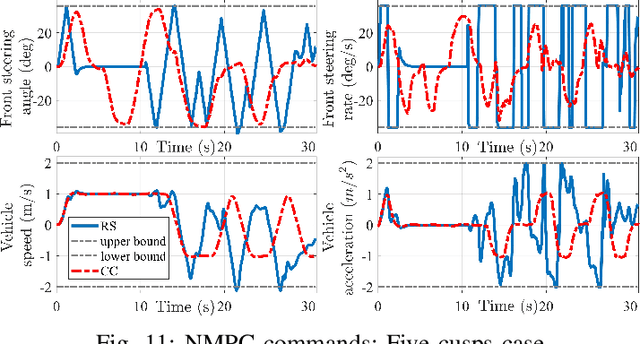
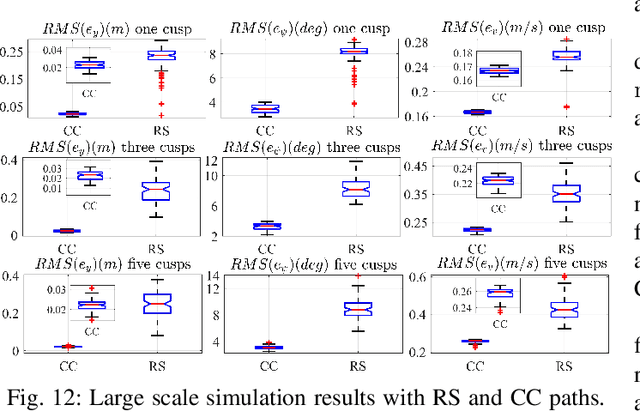
This paper investigates the planning and control for accurate positioning of car-like robots. We propose a solution that integrates two modules: a motion planner, facilitated by the rapidly-exploring random tree algorithm and continuous-curvature (CC) steering technique, generates a CC trajectory as a reference; and a nonlinear model predictive controller (NMPC) regulates the robot to accurately track the reference trajectory. Based on the $\mu$-tangency conditions in prior art, we derive explicit existence conditions and develop associated computation methods for a special class of CC paths which not only admit the same driving patterns as Reeds-Shepp paths but also consist of cusp-free clothoid turns. Afterwards, we create an autonomous vehicle parking scenario where the NMPC endeavors to follow the reference trajectory. Feasibility and computational efficiency of the CC steering are validated by numerical simulation. CarSim-Simulink joint simulations statistically verify that with exactly same NMPC, the closed-loop system with CC trajectories as references substantially outperforms the case where Reeds-Shepp trajectories are used as references.

Safe multi-agent motion planning under uncertainty for drones using filtered reinforcement learning

We consider the problem of safe multi-agent motion planning for drones in uncertain, cluttered workspaces. For this problem, we present a tractable motion planner that builds upon the strengths of reinforcement learning and constrained-control-based trajectory planning. First, we use single-agent reinforcement learning to learn motion plans from data that reach the target but may not be collision-free. Next, we use a convex optimization, chance constraints, and set-based methods for constrained control to ensure safety, despite the uncertainty in the workspace, agent motion, and sensing. The proposed approach can handle state and control constraints on the agents, and enforce collision avoidance among themselves and with static obstacles in the workspace with high probability. The proposed approach yields a safe, real-time implementable, multi-agent motion planner that is simpler to train than methods based solely on learning. Numerical simulations and experiments show the efficacy of the approach.

Approximate Dynamic Programming For Linear Systems with State and Input Constraints

Enforcing state and input constraints during reinforcement learning (RL) in continuous state spaces is an open but crucial problem which remains a roadblock to using RL in safety-critical applications. This paper leverages invariant sets to update control policies within an approximate dynamic programming (ADP) framework that guarantees constraint satisfaction for all time and converges to the optimal policy (in a linear quadratic regulator sense) asymptotically. An algorithm for implementing the proposed constrained ADP approach in a data-driven manner is provided. The potential of this formalism is demonstrated via numerical examples.