Claus Danielson
Safe On-Orbit Dislodging of Deployable Structures via Robust Adaptive MPC
Mar 21, 2025
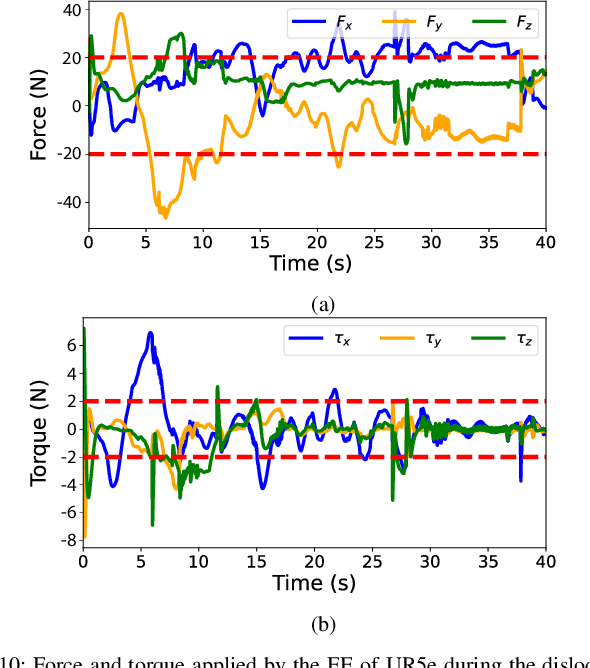


Abstract:This paper proposes a novel robust adaptive model predictive controller for on-orbit dislodging. We consider the scenario where a servicer, equipped with a robot arm, must dislodge a client, a time-varying system composed of an underpowered jammed solar panel with a hybrid hinge system on a space station. Our approach leverages online set-membership identification to reduce the uncertainty to provide robust safety guarantees during dislodging despite bounded disturbances while balancing exploration and exploitation effectively in the parameter space. The feasibility of the developed robust adaptive MPC method is also examined through dislodging simulations and hardware experiments in zero-gravity and gravity environments, respectively. In addition, the advantages of our method are shown through comparison experiments with several state-of-the-art control schemes for both accuracy of parameter estimation and control performance.
Adaptive Robot Detumbling of a Non-Rigid Satellite
Jul 24, 2024Abstract:The challenge of satellite stabilization, particularly those with uncertain flexible dynamics, has become a pressing concern in control and robotics. These uncertainties, especially the dynamics of a third-party client satellite, significantly complicate the stabilization task. This paper introduces a novel adaptive detumbling method to handle non-rigid satellites with unknown motion dynamics (translation and rotation). The distinctive feature of our approach is that we model the non-rigid tumbling satellite as a two-link serial chain with unknown stiffness and damping in contrast to previous detumbling research works which consider the satellite a rigid body. We develop a novel adaptive robotics approach to detumble the satellite by using two space tugs as servicer despite the uncertain dynamics in the post-capture case. Notably, the stiffness properties and other physical parameters, including the mass and inertia of the two links, remain unknown to the servicer. Our proposed method addresses the challenges in detumbling tasks and paves the way for advanced manipulation of non-rigid satellites with uncertain dynamics.
Decentralized Adaptive Aerospace Transportation of Unknown Loads Using A Team of Robots
Jul 10, 2024



Abstract:Transportation missions in aerospace are limited to the capability of each aerospace robot and the properties of the target transported object, such as mass, inertia, and grasping locations. We present a novel decentralized adaptive controller design for multiple robots that can be implemented in different kinds of aerospace robots. Our controller adapts to unknown objects in different gravity environments. We validate our method in an aerial scenario using multiple fully actuated hexarotors with grasping capabilities, and a space scenario using a group of space tugs. In both scenarios, the robots transport a payload cooperatively through desired three-dimensional trajectories. We show that our method can adapt to unexpected changes that include the loss of robots during the transportation mission.
Immersive Robot Programming Interface for Human-Guided Automation and Randomized Path Planning
Jun 04, 2024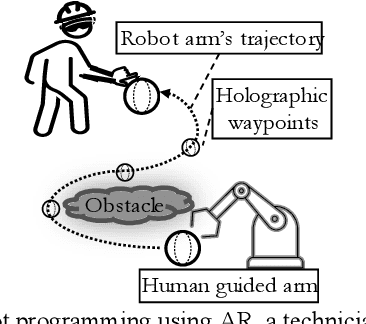
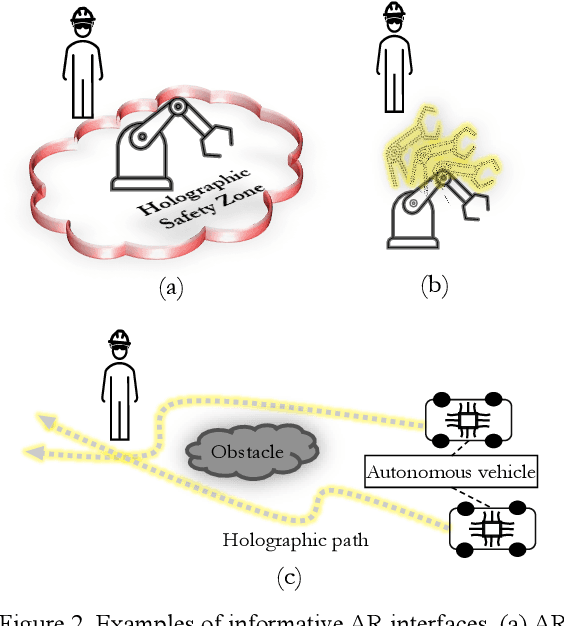
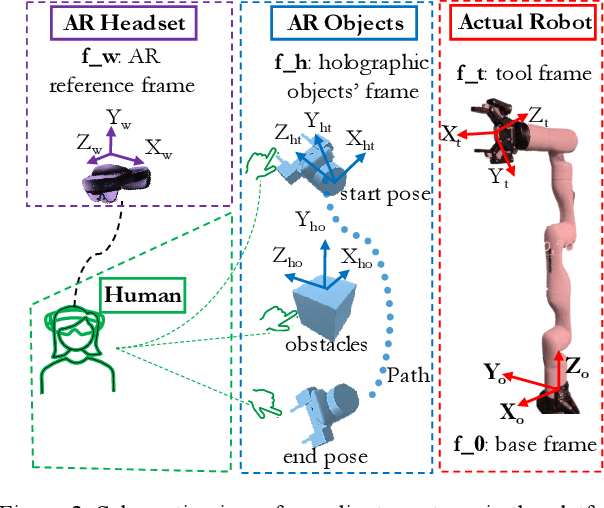
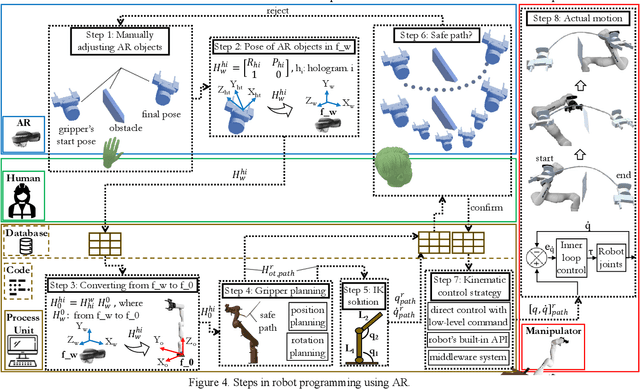
Abstract:Researchers are exploring Augmented Reality (AR) interfaces for online robot programming to streamline automation and user interaction in variable manufacturing environments. This study introduces an AR interface for online programming and data visualization that integrates the human in the randomized robot path planning, reducing the inherent randomness of the methods with human intervention. The interface uses holographic items which correspond to physical elements to interact with a redundant manipulator. Utilizing Rapidly Random Tree Star (RRT*) and Spherical Linear Interpolation (SLERP) algorithms, the interface achieves end-effector s progression through collision-free path with smooth rotation. Next, Sequential Quadratic Programming (SQP) achieve robot s configurations for this progression. The platform executes the RRT* algorithm in a loop, with each iteration independently exploring the shortest path through random sampling, leading to variations in the optimized paths produced. These paths are then demonstrated to AR users, who select the most appropriate path based on the environmental context and their intuition. The accuracy and effectiveness of the interface are validated through its implementation and testing with a seven Degree-OF-Freedom (DOF) manipulator, indicating its potential to advance current practices in robot programming. The validation of this paper include two implementations demonstrating the value of human-in-the-loop and context awareness in robotics.
Approximate Dynamic Programming For Linear Systems with State and Input Constraints
Jun 26, 2019
Abstract:Enforcing state and input constraints during reinforcement learning (RL) in continuous state spaces is an open but crucial problem which remains a roadblock to using RL in safety-critical applications. This paper leverages invariant sets to update control policies within an approximate dynamic programming (ADP) framework that guarantees constraint satisfaction for all time and converges to the optimal policy (in a linear quadratic regulator sense) asymptotically. An algorithm for implementing the proposed constrained ADP approach in a data-driven manner is provided. The potential of this formalism is demonstrated via numerical examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge