In Defense of the Unitary Scalarization for Deep Multi-Task Learning
Paper and Code
Jan 20, 2022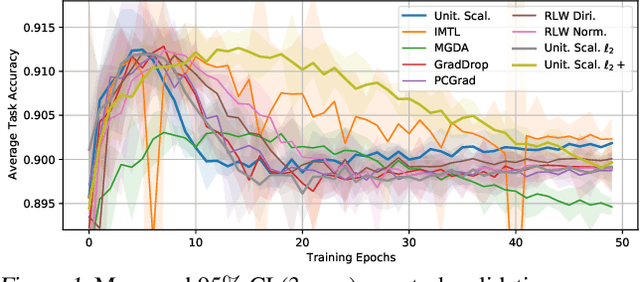


Recent multi-task learning research argues against unitary scalarization, where training simply minimizes the sum of the task losses. Several ad-hoc multi-task optimization algorithms have instead been proposed, inspired by various hypotheses about what makes multi-task settings difficult. The majority of these optimizers require per-task gradients, and introduce significant memory, runtime, and implementation overhead. We present a theoretical analysis suggesting that many specialized multi-task optimizers can be interpreted as forms of regularization. Moreover, we show that, when coupled with standard regularization and stabilization techniques from single-task learning, unitary scalarization matches or improves upon the performance of complex multi-task optimizers in both supervised and reinforcement learning settings. We believe our results call for a critical reevaluation of recent research in the area.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge