Concept Boundary Vectors

Machine learning models are trained with relatively simple objectives, such as next token prediction. However, on deployment, they appear to capture a more fundamental representation of their input data. It is of interest to understand the nature of these representations to help interpret the model's outputs and to identify ways to improve the salience of these representations. Concept vectors are constructions aimed at attributing concepts in the input data to directions, represented by vectors, in the model's latent space. In this work, we introduce concept boundary vectors as a concept vector construction derived from the boundary between the latent representations of concepts. Empirically we demonstrate that concept boundary vectors capture a concept's semantic meaning, and we compare their effectiveness against concept activation vectors.

Spatially-Adaptive Hash Encodings For Neural Surface Reconstruction

Positional encodings are a common component of neural scene reconstruction methods, and provide a way to bias the learning of neural fields towards coarser or finer representations. Current neural surface reconstruction methods use a "one-size-fits-all" approach to encoding, choosing a fixed set of encoding functions, and therefore bias, across all scenes. Current state-of-the-art surface reconstruction approaches leverage grid-based multi-resolution hash encoding in order to recover high-detail geometry. We propose a learned approach which allows the network to choose its encoding basis as a function of space, by masking the contribution of features stored at separate grid resolutions. The resulting spatially adaptive approach allows the network to fit a wider range of frequencies without introducing noise. We test our approach on standard benchmark surface reconstruction datasets and achieve state-of-the-art performance on two benchmark datasets.

CrossSDF: 3D Reconstruction of Thin Structures From Cross-Sections

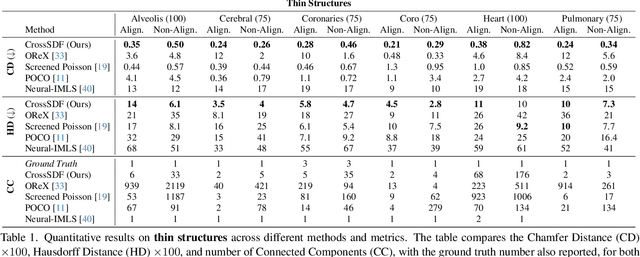
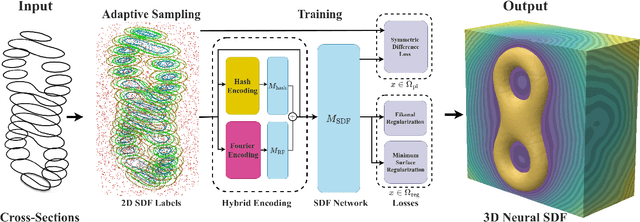
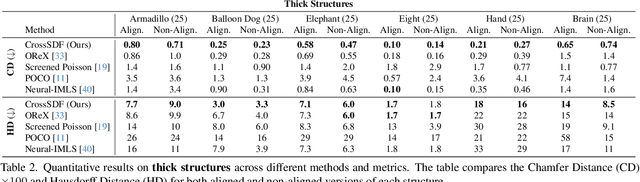
Reconstructing complex structures from planar cross-sections is a challenging problem, with wide-reaching applications in medical imaging, manufacturing, and topography. Out-of-the-box point cloud reconstruction methods can often fail due to the data sparsity between slicing planes, while current bespoke methods struggle to reconstruct thin geometric structures and preserve topological continuity. This is important for medical applications where thin vessel structures are present in CT and MRI scans. This paper introduces \method, a novel approach for extracting a 3D signed distance field from 2D signed distances generated from planar contours. Our approach makes the training of neural SDFs contour-aware by using losses designed for the case where geometry is known within 2D slices. Our results demonstrate a significant improvement over existing methods, effectively reconstructing thin structures and producing accurate 3D models without the interpolation artifacts or over-smoothing of prior approaches.

Tightening the Evaluation of PAC Bounds Using Formal Verification Results

Probably Approximately Correct (PAC) bounds are widely used to derive probabilistic guarantees for the generalisation of machine learning models. They highlight the components of the model which contribute to its generalisation capacity. However, current state-of-the-art results are loose in approximating the generalisation capacity of deployed machine learning models. Consequently, while PAC bounds are theoretically useful, their applicability for evaluating a model's generalisation property in a given operational design domain is limited. The underlying classical theory is supported by the idea that bounds can be tightened when the number of test points available to the user to evaluate the model increases. Yet, in the case of neural networks, the number of test points required to obtain bounds of interest is often impractical even for small problems. In this paper, we take the novel approach of using the formal verification of neural systems to inform the evaluation of PAC bounds. Rather than using pointwise information obtained from repeated tests, we use verification results on regions around test points. We show that conditioning existing bounds on verification results leads to a tightening proportional to the underlying probability mass of the verified region.

Spherical Feature Pyramid Networks For Semantic Segmentation

Semantic segmentation for spherical data is a challenging problem in machine learning since conventional planar approaches require projecting the spherical image to the Euclidean plane. Representing the signal on a fundamentally different topology introduces edges and distortions which impact network performance. Recently, graph-based approaches have bypassed these challenges to attain significant improvements by representing the signal on a spherical mesh. Current approaches to spherical segmentation exclusively use variants of the UNet architecture, meaning more successful planar architectures remain unexplored. Inspired by the success of feature pyramid networks (FPNs) in planar image segmentation, we leverage the pyramidal hierarchy of graph-based spherical CNNs to design spherical FPNs. Our spherical FPN models show consistent improvements over spherical UNets, whilst using fewer parameters. On the Stanford 2D-3D-S dataset, our models achieve state-of-the-art performance with an mIOU of 48.75, an improvement of 3.75 IoU points over the previous best spherical CNN.

Explicit Neural Surfaces: Learning Continuous Geometry With Deformation Fields

We introduce Explicit Neural Surfaces (ENS), an efficient surface reconstruction method that learns an explicitly defined continuous surface from multiple views. We use a series of neural deformation fields to progressively transform a continuous input surface to a target shape. By sampling meshes as discrete surface proxies, we train the deformation fields through efficient differentiable rasterization, and attain a mesh-independent and smooth surface representation. By using Laplace-Beltrami eigenfunctions as an intrinsic positional encoding alongside standard extrinsic Fourier features, our approach can capture fine surface details. ENS trains 1 to 2 orders of magnitude faster and can extract meshes of higher quality compared to implicit representations, whilst maintaining competitive surface reconstruction performance and real-time capabilities. Finally, we apply our approach to learn a collection of objects in a single model, and achieve disentangled interpolations between different shapes, their surface details, and textures.