Spatially-Adaptive Hash Encodings For Neural Surface Reconstruction

Positional encodings are a common component of neural scene reconstruction methods, and provide a way to bias the learning of neural fields towards coarser or finer representations. Current neural surface reconstruction methods use a "one-size-fits-all" approach to encoding, choosing a fixed set of encoding functions, and therefore bias, across all scenes. Current state-of-the-art surface reconstruction approaches leverage grid-based multi-resolution hash encoding in order to recover high-detail geometry. We propose a learned approach which allows the network to choose its encoding basis as a function of space, by masking the contribution of features stored at separate grid resolutions. The resulting spatially adaptive approach allows the network to fit a wider range of frequencies without introducing noise. We test our approach on standard benchmark surface reconstruction datasets and achieve state-of-the-art performance on two benchmark datasets.

CrossSDF: 3D Reconstruction of Thin Structures From Cross-Sections

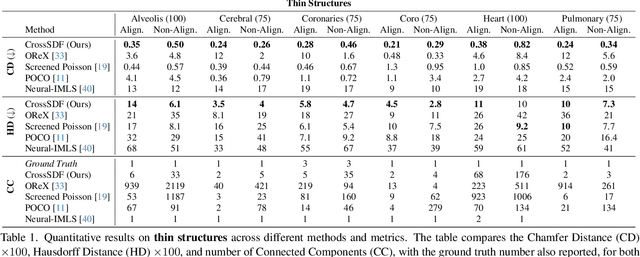
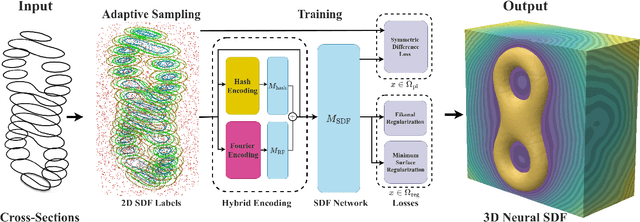
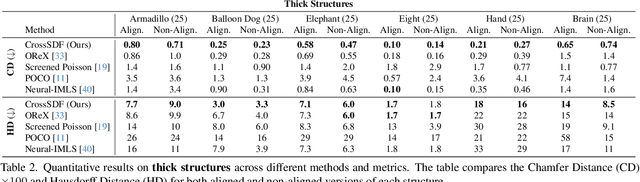
Reconstructing complex structures from planar cross-sections is a challenging problem, with wide-reaching applications in medical imaging, manufacturing, and topography. Out-of-the-box point cloud reconstruction methods can often fail due to the data sparsity between slicing planes, while current bespoke methods struggle to reconstruct thin geometric structures and preserve topological continuity. This is important for medical applications where thin vessel structures are present in CT and MRI scans. This paper introduces \method, a novel approach for extracting a 3D signed distance field from 2D signed distances generated from planar contours. Our approach makes the training of neural SDFs contour-aware by using losses designed for the case where geometry is known within 2D slices. Our results demonstrate a significant improvement over existing methods, effectively reconstructing thin structures and producing accurate 3D models without the interpolation artifacts or over-smoothing of prior approaches.

Explicit Neural Surfaces: Learning Continuous Geometry With Deformation Fields

We introduce Explicit Neural Surfaces (ENS), an efficient surface reconstruction method that learns an explicitly defined continuous surface from multiple views. We use a series of neural deformation fields to progressively transform a continuous input surface to a target shape. By sampling meshes as discrete surface proxies, we train the deformation fields through efficient differentiable rasterization, and attain a mesh-independent and smooth surface representation. By using Laplace-Beltrami eigenfunctions as an intrinsic positional encoding alongside standard extrinsic Fourier features, our approach can capture fine surface details. ENS trains 1 to 2 orders of magnitude faster and can extract meshes of higher quality compared to implicit representations, whilst maintaining competitive surface reconstruction performance and real-time capabilities. Finally, we apply our approach to learn a collection of objects in a single model, and achieve disentangled interpolations between different shapes, their surface details, and textures.

OReX: Object Reconstruction from Planner Cross-sections Using Neural Fields

Reconstructing 3D shapes from planar cross-sections is a challenge inspired by downstream applications like medical imaging and geographic informatics. The input is an in/out indicator function fully defined on a sparse collection of planes in space, and the output is an interpolation of the indicator function to the entire volume. Previous works addressing this sparse and ill-posed problem either produce low quality results, or rely on additional priors such as target topology, appearance information, or input normal directions. In this paper, we present OReX, a method for 3D shape reconstruction from slices alone, featuring a Neural Field as the interpolation prior. A simple neural network is trained on the input planes to receive a 3D coordinate and return an inside/outside estimate for the query point. This prior is powerful in inducing smoothness and self-similarities. The main challenge for this approach is high-frequency details, as the neural prior is overly smoothing. To alleviate this, we offer an iterative estimation architecture and a hierarchical input sampling scheme that encourage coarse-to-fine training, allowing focusing on high frequencies at later stages. In addition, we identify and analyze a common ripple-like effect stemming from the mesh extraction step. We mitigate it by regularizing the spatial gradients of the indicator function around input in/out boundaries, cutting the problem at the root. Through extensive qualitative and quantitative experimentation, we demonstrate our method is robust, accurate, and scales well with the size of the input. We report state-of-the-art results compared to previous approaches and recent potential solutions, and demonstrate the benefit of our individual contributions through analysis and ablation studies.