Spherical Voronoi: Directional Appearance as a Differentiable Partition of the Sphere

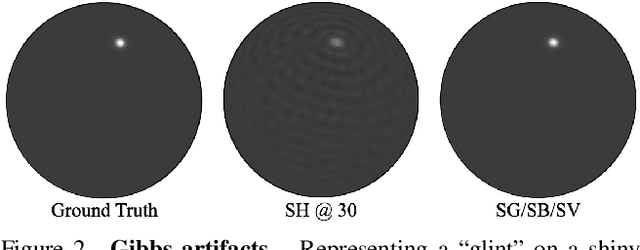
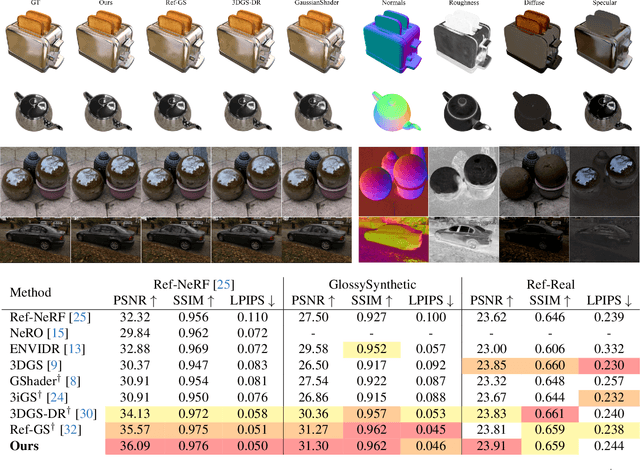
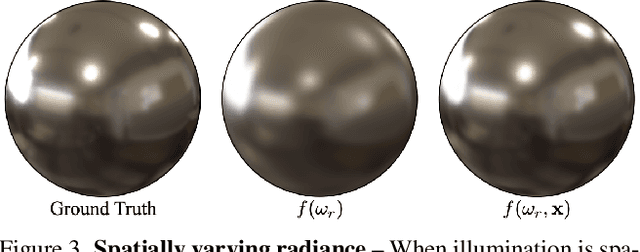
Radiance field methods (e.g. 3D Gaussian Splatting) have emerged as a powerful paradigm for novel view synthesis, yet their appearance modeling often relies on Spherical Harmonics (SH), which impose fundamental limitations. SH struggle with high-frequency signals, exhibit Gibbs ringing artifacts, and fail to capture specular reflections - a key component of realistic rendering. Although alternatives like spherical Gaussians offer improvements, they add significant optimization complexity. We propose Spherical Voronoi (SV) as a unified framework for appearance representation in 3D Gaussian Splatting. SV partitions the directional domain into learnable regions with smooth boundaries, providing an intuitive and stable parameterization for view-dependent effects. For diffuse appearance, SV achieves competitive results while keeping optimization simpler than existing alternatives. For reflections - where SH fail - we leverage SV as learnable reflection probes, taking reflected directions as input following principles from classical graphics. This formulation attains state-of-the-art results on synthetic and real-world datasets, demonstrating that SV offers a principled, efficient, and general solution for appearance modeling in explicit 3D representations.

Nexels: Neurally-Textured Surfels for Real-Time Novel View Synthesis with Sparse Geometries

Though Gaussian splatting has achieved impressive results in novel view synthesis, it requires millions of primitives to model highly textured scenes, even when the geometry of the scene is simple. We propose a representation that goes beyond point-based rendering and decouples geometry and appearance in order to achieve a compact representation. We use surfels for geometry and a combination of a global neural field and per-primitive colours for appearance. The neural field textures a fixed number of primitives for each pixel, ensuring that the added compute is low. Our representation matches the perceptual quality of 3D Gaussian splatting while using $9.7\times$ fewer primitives and $5.5\times$ less memory on outdoor scenes and using $31\times$ fewer primitives and $3.7\times$ less memory on indoor scenes. Our representation also renders twice as fast as existing textured primitives while improving upon their visual quality.

ROOM: A Physics-Based Continuum Robot Simulator for Photorealistic Medical Datasets Generation

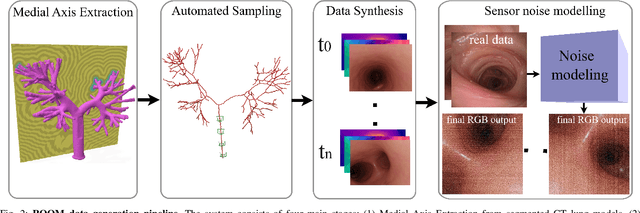
Continuum robots are advancing bronchoscopy procedures by accessing complex lung airways and enabling targeted interventions. However, their development is limited by the lack of realistic training and test environments: Real data is difficult to collect due to ethical constraints and patient safety concerns, and developing autonomy algorithms requires realistic imaging and physical feedback. We present ROOM (Realistic Optical Observation in Medicine), a comprehensive simulation framework designed for generating photorealistic bronchoscopy training data. By leveraging patient CT scans, our pipeline renders multi-modal sensor data including RGB images with realistic noise and light specularities, metric depth maps, surface normals, optical flow and point clouds at medically relevant scales. We validate the data generated by ROOM in two canonical tasks for medical robotics -- multi-view pose estimation and monocular depth estimation, demonstrating diverse challenges that state-of-the-art methods must overcome to transfer to these medical settings. Furthermore, we show that the data produced by ROOM can be used to fine-tune existing depth estimation models to overcome these challenges, also enabling other downstream applications such as navigation. We expect that ROOM will enable large-scale data generation across diverse patient anatomies and procedural scenarios that are challenging to capture in clinical settings. Code and data: https://github.com/iamsalvatore/room.

NoKSR: Kernel-Free Neural Surface Reconstruction via Point Cloud Serialization

We present a novel approach to large-scale point cloud surface reconstruction by developing an efficient framework that converts an irregular point cloud into a signed distance field (SDF). Our backbone builds upon recent transformer-based architectures (i.e., PointTransformerV3), that serializes the point cloud into a locality-preserving sequence of tokens. We efficiently predict the SDF value at a point by aggregating nearby tokens, where fast approximate neighbors can be retrieved thanks to the serialization. We serialize the point cloud at different levels/scales, and non-linearly aggregate a feature to predict the SDF value. We show that aggregating across multiple scales is critical to overcome the approximations introduced by the serialization (i.e. false negatives in the neighborhood). Our frameworks sets the new state-of-the-art in terms of accuracy and efficiency (better or similar performance with half the latency of the best prior method, coupled with a simpler implementation), particularly on outdoor datasets where sparse-grid methods have shown limited performance.

Radiant Foam: Real-Time Differentiable Ray Tracing

Research on differentiable scene representations is consistently moving towards more efficient, real-time models. Recently, this has led to the popularization of splatting methods, which eschew the traditional ray-based rendering of radiance fields in favor of rasterization. This has yielded a significant improvement in rendering speeds due to the efficiency of rasterization algorithms and hardware, but has come at a cost: the approximations that make rasterization efficient also make implementation of light transport phenomena like reflection and refraction much more difficult. We propose a novel scene representation which avoids these approximations, but keeps the efficiency and reconstruction quality of splatting by leveraging a decades-old efficient volumetric mesh ray tracing algorithm which has been largely overlooked in recent computer vision research. The resulting model, which we name Radiant Foam, achieves rendering speed and quality comparable to Gaussian Splatting, without the constraints of rasterization. Unlike ray traced Gaussian models that use hardware ray tracing acceleration, our method requires no special hardware or APIs beyond the standard features of a programmable GPU.

CrossSDF: 3D Reconstruction of Thin Structures From Cross-Sections

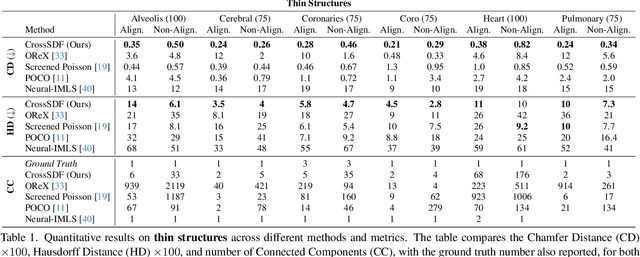
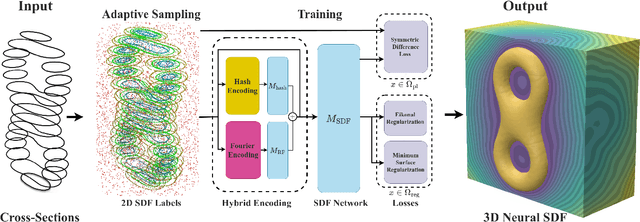
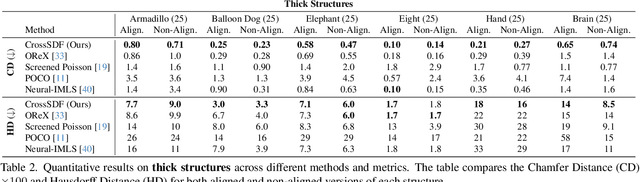
Reconstructing complex structures from planar cross-sections is a challenging problem, with wide-reaching applications in medical imaging, manufacturing, and topography. Out-of-the-box point cloud reconstruction methods can often fail due to the data sparsity between slicing planes, while current bespoke methods struggle to reconstruct thin geometric structures and preserve topological continuity. This is important for medical applications where thin vessel structures are present in CT and MRI scans. This paper introduces \method, a novel approach for extracting a 3D signed distance field from 2D signed distances generated from planar contours. Our approach makes the training of neural SDFs contour-aware by using losses designed for the case where geometry is known within 2D slices. Our results demonstrate a significant improvement over existing methods, effectively reconstructing thin structures and producing accurate 3D models without the interpolation artifacts or over-smoothing of prior approaches.

Lagrangian Hashing for Compressed Neural Field Representations

We present Lagrangian Hashing, a representation for neural fields combining the characteristics of fast training NeRF methods that rely on Eulerian grids (i.e.~InstantNGP), with those that employ points equipped with features as a way to represent information (e.g. 3D Gaussian Splatting or PointNeRF). We achieve this by incorporating a point-based representation into the high-resolution layers of the hierarchical hash tables of an InstantNGP representation. As our points are equipped with a field of influence, our representation can be interpreted as a mixture of Gaussians stored within the hash table. We propose a loss that encourages the movement of our Gaussians towards regions that require more representation budget to be sufficiently well represented. Our main finding is that our representation allows the reconstruction of signals using a more compact representation without compromising quality.

LSE-NeRF: Learning Sensor Modeling Errors for Deblured Neural Radiance Fields with RGB-Event Stereo

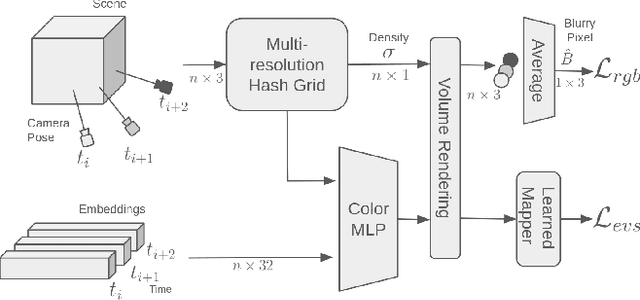
We present a method for reconstructing a clear Neural Radiance Field (NeRF) even with fast camera motions. To address blur artifacts, we leverage both (blurry) RGB images and event camera data captured in a binocular configuration. Importantly, when reconstructing our clear NeRF, we consider the camera modeling imperfections that arise from the simple pinhole camera model as learned embeddings for each camera measurement, and further learn a mapper that connects event camera measurements with RGB data. As no previous dataset exists for our binocular setting, we introduce an event camera dataset with captures from a 3D-printed stereo configuration between RGB and event cameras. Empirically, we evaluate our introduced dataset and EVIMOv2 and show that our method leads to improved reconstructions. Our code and dataset are available at https://github.com/ubc-vision/LSENeRF.

BANF: Band-limited Neural Fields for Levels of Detail Reconstruction

Largely due to their implicit nature, neural fields lack a direct mechanism for filtering, as Fourier analysis from discrete signal processing is not directly applicable to these representations. Effective filtering of neural fields is critical to enable level-of-detail processing in downstream applications, and support operations that involve sampling the field on regular grids (e.g. marching cubes). Existing methods that attempt to decompose neural fields in the frequency domain either resort to heuristics or require extensive modifications to the neural field architecture. We show that via a simple modification, one can obtain neural fields that are low-pass filtered, and in turn show how this can be exploited to obtain a frequency decomposition of the entire signal. We demonstrate the validity of our technique by investigating level-of-detail reconstruction, and showing how coarser representations can be computed effectively.

Does Gaussian Splatting need SFM Initialization?

3D Gaussian Splatting has recently been embraced as a versatile and effective method for scene reconstruction and novel view synthesis, owing to its high-quality results and compatibility with hardware rasterization. Despite its advantages, Gaussian Splatting's reliance on high-quality point cloud initialization by Structure-from-Motion (SFM) algorithms is a significant limitation to be overcome. To this end, we investigate various initialization strategies for Gaussian Splatting and delve into how volumetric reconstructions from Neural Radiance Fields (NeRF) can be utilized to bypass the dependency on SFM data. Our findings demonstrate that random initialization can perform much better if carefully designed and that by employing a combination of improved initialization strategies and structure distillation from low-cost NeRF models, it is possible to achieve equivalent results, or at times even superior, to those obtained from SFM initialization.