Jeff Tseng
3D Gaussian Splatting as Markov Chain Monte Carlo
Apr 15, 2024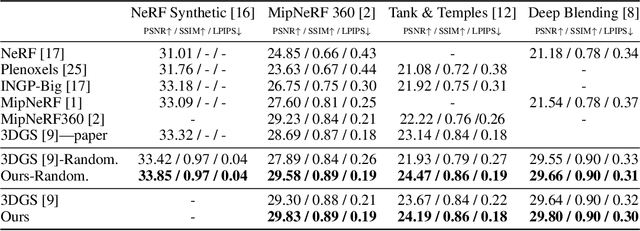


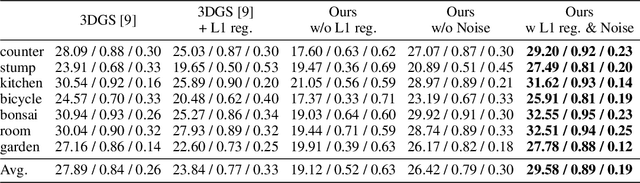
Abstract:While 3D Gaussian Splatting has recently become popular for neural rendering, current methods rely on carefully engineered cloning and splitting strategies for placing Gaussians, which does not always generalize and may lead to poor-quality renderings. In addition, for real-world scenes, they rely on a good initial point cloud to perform well. In this work, we rethink 3D Gaussians as random samples drawn from an underlying probability distribution describing the physical representation of the scene -- in other words, Markov Chain Monte Carlo (MCMC) samples. Under this view, we show that the 3D Gaussian updates are strikingly similar to a Stochastic Langevin Gradient Descent (SGLD) update. As with MCMC, samples are nothing but past visit locations, adding new Gaussians under our framework can simply be realized without heuristics as placing Gaussians at existing Gaussian locations. To encourage using fewer Gaussians for efficiency, we introduce an L1-regularizer on the Gaussians. On various standard evaluation scenes, we show that our method provides improved rendering quality, easy control over the number of Gaussians, and robustness to initialization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge