StochasticSplats: Stochastic Rasterization for Sorting-Free 3D Gaussian Splatting

3D Gaussian splatting (3DGS) is a popular radiance field method, with many application-specific extensions. Most variants rely on the same core algorithm: depth-sorting of Gaussian splats then rasterizing in primitive order. This ensures correct alpha compositing, but can cause rendering artifacts due to built-in approximations. Moreover, for a fixed representation, sorted rendering offers little control over render cost and visual fidelity. For example, and counter-intuitively, rendering a lower-resolution image is not necessarily faster. In this work, we address the above limitations by combining 3D Gaussian splatting with stochastic rasterization. Concretely, we leverage an unbiased Monte Carlo estimator of the volume rendering equation. This removes the need for sorting, and allows for accurate 3D blending of overlapping Gaussians. The number of Monte Carlo samples further imbues 3DGS with a way to trade off computation time and quality. We implement our method using OpenGL shaders, enabling efficient rendering on modern GPU hardware. At a reasonable visual quality, our method renders more than four times faster than sorted rasterization.

3D Gaussian Splatting as Markov Chain Monte Carlo

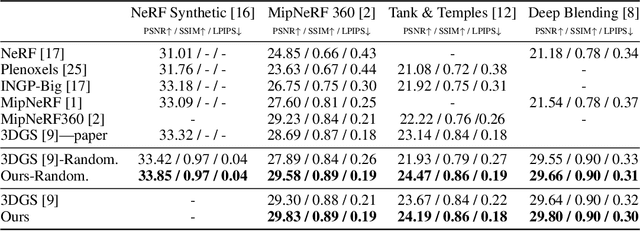
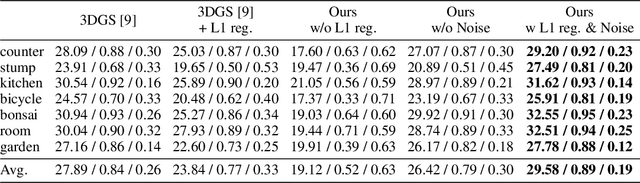
While 3D Gaussian Splatting has recently become popular for neural rendering, current methods rely on carefully engineered cloning and splitting strategies for placing Gaussians, which does not always generalize and may lead to poor-quality renderings. In addition, for real-world scenes, they rely on a good initial point cloud to perform well. In this work, we rethink 3D Gaussians as random samples drawn from an underlying probability distribution describing the physical representation of the scene -- in other words, Markov Chain Monte Carlo (MCMC) samples. Under this view, we show that the 3D Gaussian updates are strikingly similar to a Stochastic Langevin Gradient Descent (SGLD) update. As with MCMC, samples are nothing but past visit locations, adding new Gaussians under our framework can simply be realized without heuristics as placing Gaussians at existing Gaussian locations. To encourage using fewer Gaussians for efficiency, we introduce an L1-regularizer on the Gaussians. On various standard evaluation scenes, we show that our method provides improved rendering quality, easy control over the number of Gaussians, and robustness to initialization.

Accelerating Neural Field Training via Soft Mining

We present an approach to accelerate Neural Field training by efficiently selecting sampling locations. While Neural Fields have recently become popular, it is often trained by uniformly sampling the training domain, or through handcrafted heuristics. We show that improved convergence and final training quality can be achieved by a soft mining technique based on importance sampling: rather than either considering or ignoring a pixel completely, we weigh the corresponding loss by a scalar. To implement our idea we use Langevin Monte-Carlo sampling. We show that by doing so, regions with higher error are being selected more frequently, leading to more than 2x improvement in convergence speed. The code and related resources for this study are publicly available at https://ubc-vision.github.io/nf-soft-mining/.

Preimplantation Blastomere Boundary Identification in HMC Microscopic Images of Early Stage Human Embryos

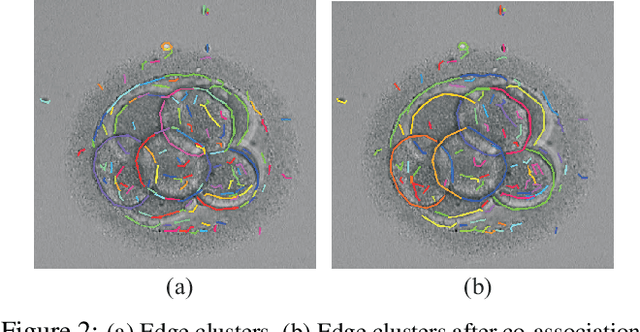
We present a novel method for identification of the boundary of embryonic cells (blastomeres) in Hoffman Modulation Contrast (HMC) microscopic images that are taken between day one to day three. Identification of boundaries of blastomeres is a challenging task, especially in the cases containing four or more cells. This is because these cells are bundled up tightly inside an embryo's membrane and any 2D image projection of such 3D embryo includes cell overlaps, occlusions, and projection ambiguities. Moreover, human embryos include fragmentation, which does not conform to any specific patterns or shape. Here we developed a model-based iterative approach, in which blastomeres are modeled as ellipses that conform to the local image features, such as edges and normals. In an iterative process, each image feature contributes only to one candidate and is removed upon being associated to a model candidate. We have tested the proposed algorithm on an image dataset comprising of 468 human embryos obtained from different sources. An overall Precision, Sensitivity and Overall Quality (OQ) of 92%, 88% and 83% are achieved.