Francesca Cairoli
CoCAI: Copula-based Conformal Anomaly Identification for Multivariate Time-Series
Jul 23, 2025Abstract:We propose a novel framework that harnesses the power of generative artificial intelligence and copula-based modeling to address two critical challenges in multivariate time-series analysis: delivering accurate predictions and enabling robust anomaly detection. Our method, Copula-based Conformal Anomaly Identification for Multivariate Time-Series (CoCAI), leverages a diffusion-based model to capture complex dependencies within the data, enabling high quality forecasting. The model's outputs are further calibrated using a conformal prediction technique, yielding predictive regions which are statistically valid, i.e., cover the true target values with a desired confidence level. Starting from these calibrated forecasts, robust outlier detection is performed by combining dimensionality reduction techniques with copula-based modeling, providing a statistically grounded anomaly score. CoCAI benefits from an offline calibration phase that allows for minimal overhead during deployment and delivers actionable results rooted in established theoretical foundations. Empirical tests conducted on real operational data derived from water distribution and sewerage systems confirm CoCAI's effectiveness in accurately forecasting target sequences of data and in identifying anomalous segments within them.
Diffusion-based Time Series Forecasting for Sewerage Systems
Jun 10, 2025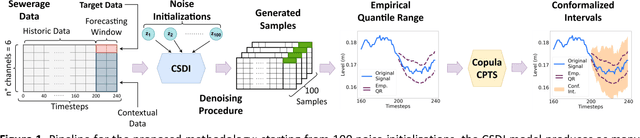
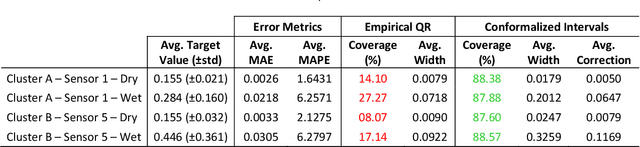
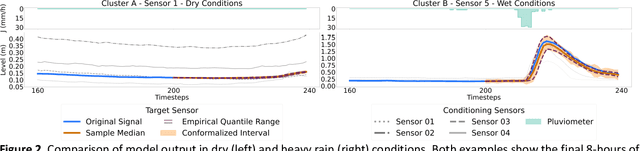
Abstract:We introduce a novel deep learning approach that harnesses the power of generative artificial intelligence to enhance the accuracy of contextual forecasting in sewerage systems. By developing a diffusion-based model that processes multivariate time series data, our system excels at capturing complex correlations across diverse environmental signals, enabling robust predictions even during extreme weather events. To strengthen the model's reliability, we further calibrate its predictions with a conformal inference technique, tailored for probabilistic time series data, ensuring that the resulting prediction intervals are statistically reliable and cover the true target values with a desired confidence level. Our empirical tests on real sewerage system data confirm the model's exceptional capability to deliver reliable contextual predictions, maintaining accuracy even under severe weather conditions.
Learning-Based Approaches to Predictive Monitoring with Conformal Statistical Guarantees
Dec 04, 2023Abstract:This tutorial focuses on efficient methods to predictive monitoring (PM), the problem of detecting at runtime future violations of a given requirement from the current state of a system. While performing model checking at runtime would offer a precise solution to the PM problem, it is generally computationally expensive. To address this scalability issue, several lightweight approaches based on machine learning have recently been proposed. These approaches work by learning an approximate yet efficient surrogate (deep learning) model of the expensive model checker. A key challenge remains to ensure reliable predictions, especially in safety-critical applications. We review our recent work on predictive monitoring, one of the first to propose learning-based approximations for CPS verification of temporal logic specifications and the first in this context to apply conformal prediction (CP) for rigorous uncertainty quantification. These CP-based uncertainty estimators offer statistical guarantees regarding the generalization error of the learning model, and they can be used to determine unreliable predictions that should be rejected. In this tutorial, we present a general and comprehensive framework summarizing our approach to the predictive monitoring of CPSs, examining in detail several variants determined by three main dimensions: system dynamics (deterministic, non-deterministic, stochastic), state observability, and semantics of requirements' satisfaction (Boolean or quantitative).
Conformal Quantitative Predictive Monitoring of STL Requirements for Stochastic Processes
Nov 04, 2022



Abstract:We consider the problem of predictive monitoring (PM), i.e., predicting at runtime the satisfaction of a desired property from the current system's state. Due to its relevance for runtime safety assurance and online control, PM methods need to be efficient to enable timely interventions against predicted violations, while providing correctness guarantees. We introduce \textit{quantitative predictive monitoring (QPM)}, the first PM method to support stochastic processes and rich specifications given in Signal Temporal Logic (STL). Unlike most of the existing PM techniques that predict whether or not some property $\phi$ is satisfied, QPM provides a quantitative measure of satisfaction by predicting the quantitative (aka robust) STL semantics of $\phi$. QPM derives prediction intervals that are highly efficient to compute and with probabilistic guarantees, in that the intervals cover with arbitrary probability the STL robustness values relative to the stochastic evolution of the system. To do so, we take a machine-learning approach and leverage recent advances in conformal inference for quantile regression, thereby avoiding expensive Monte-Carlo simulations at runtime to estimate the intervals. We also show how our monitors can be combined in a compositional manner to handle composite formulas, without retraining the predictors nor sacrificing the guarantees. We demonstrate the effectiveness and scalability of QPM over a benchmark of four discrete-time stochastic processes with varying degrees of complexity.
Stochastic Variational Smoothed Model Checking
May 11, 2022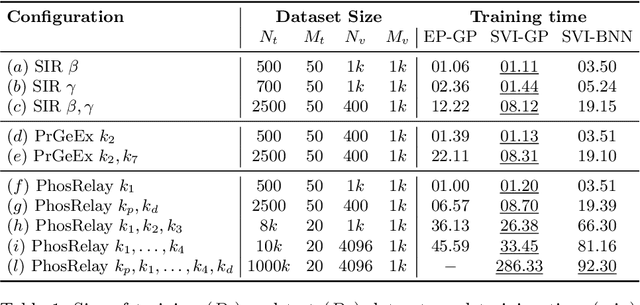

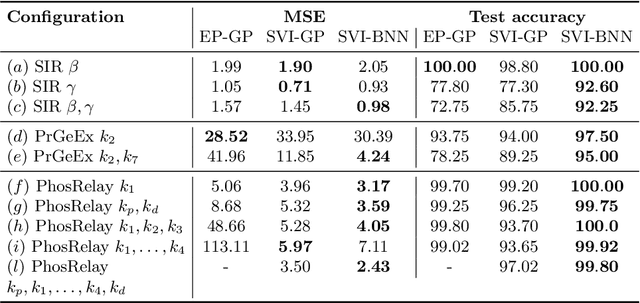

Abstract:Model-checking for parametric stochastic models can be expressed as checking the satisfaction probability of a certain property as a function of the parameters of the model. Smoothed model checking (smMC) leverages Gaussian Processes (GP) to infer the satisfaction function over the entire parameter space from a limited set of observations obtained via simulation. This approach provides accurate reconstructions with statistically sound quantification of the uncertainty. However, it inherits the scalability issues of GP. In this paper, we exploit recent advances in probabilistic machine learning to push this limitation forward, making Bayesian inference of smMC scalable to larger datasets, enabling its application to larger models in terms of the dimension of the parameter set. We propose Stochastic Variational Smoothed Model Checking (SV-smMC), a solution that exploits stochastic variational inference (SVI) to approximate the posterior distribution of the smMC problem. The strength and flexibility of SVI make SV-smMC applicable to two alternative probabilistic models: Gaussian Processes (GP) and Bayesian Neural Networks (BNN). Moreover, SVI makes inference easily parallelizable and it enables GPU acceleration. In this paper, we compare the performances of smMC against those of SV-smMC by looking at the scalability, the computational efficiency and at the accuracy of the reconstructed satisfaction function.
Neural Predictive Monitoring under Partial Observability
Aug 17, 2021



Abstract:We consider the problem of predictive monitoring (PM), i.e., predicting at runtime future violations of a system from the current state. We work under the most realistic settings where only partial and noisy observations of the state are available at runtime. Such settings directly affect the accuracy and reliability of the reachability predictions, jeopardizing the safety of the system. In this work, we present a learning-based method for PM that produces accurate and reliable reachability predictions despite partial observability (PO). We build on Neural Predictive Monitoring (NPM), a PM method that uses deep neural networks for approximating hybrid systems reachability, and extend it to the PO case. We propose and compare two solutions, an end-to-end approach, which directly operates on the rough observations, and a two-step approach, which introduces an intermediate state estimation step. Both solutions rely on conformal prediction to provide 1) probabilistic guarantees in the form of prediction regions and 2) sound estimates of predictive uncertainty. We use the latter to identify unreliable (and likely erroneous) predictions and to retrain and improve the monitors on these uncertain inputs (i.e., active learning). Our method results in highly accurate reachability predictions and error detection, as well as tight prediction regions with guaranteed coverage.
Abstraction of Markov Population Dynamics via Generative Adversarial Nets
Jun 24, 2021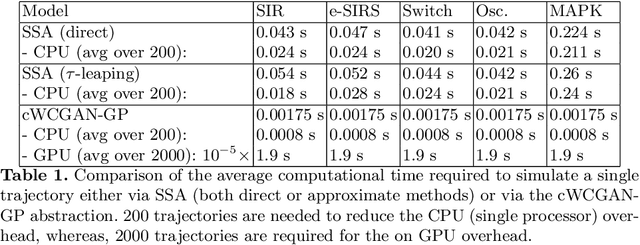
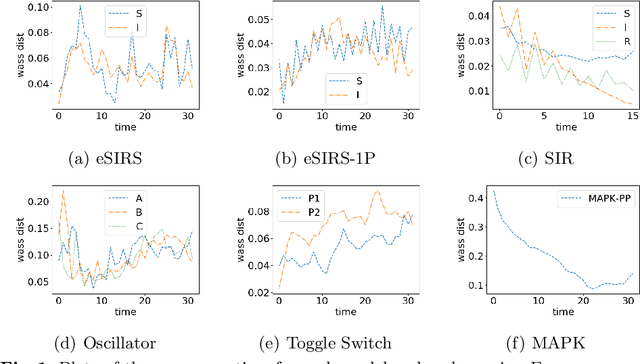
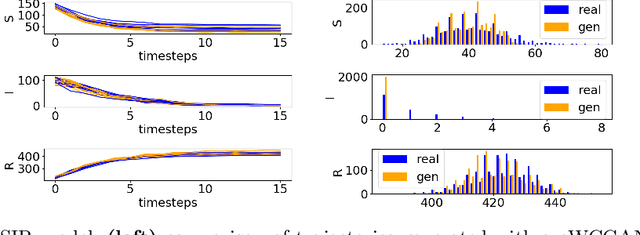
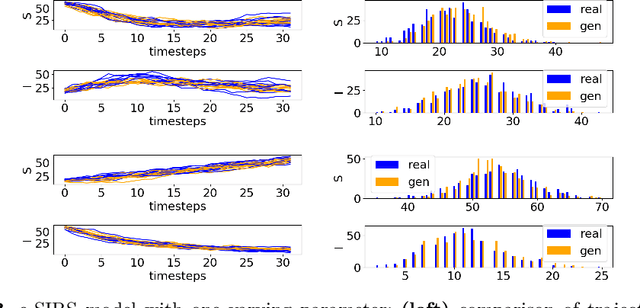
Abstract:Markov Population Models are a widespread formalism used to model the dynamics of complex systems, with applications in Systems Biology and many other fields. The associated Markov stochastic process in continuous time is often analyzed by simulation, which can be costly for large or stiff systems, particularly when a massive number of simulations has to be performed (e.g. in a multi-scale model). A strategy to reduce computational load is to abstract the population model, replacing it with a simpler stochastic model, faster to simulate. Here we pursue this idea, building on previous works and constructing a generator capable of producing stochastic trajectories in continuous space and discrete time. This generator is learned automatically from simulations of the original model in a Generative Adversarial setting. Compared to previous works, which rely on deep neural networks and Dirichlet processes, we explore the use of state of the art generative models, which are flexible enough to learn a full trajectory rather than a single transition kernel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge