Paolo Pulcini
Stochastic Variational Smoothed Model Checking
May 11, 2022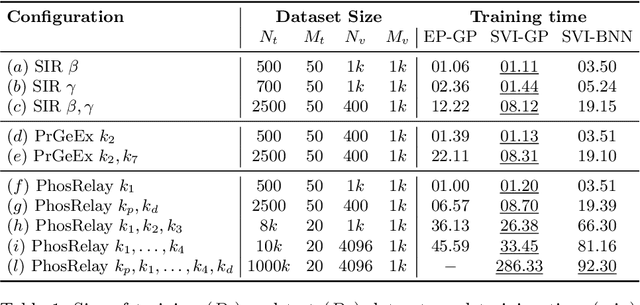

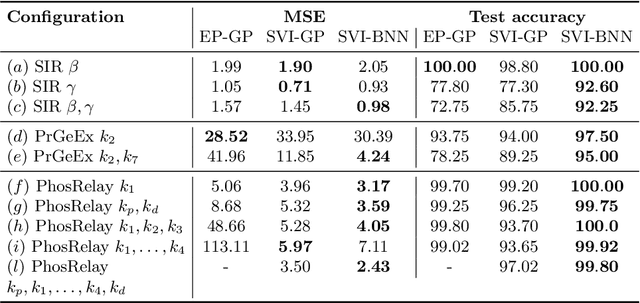

Abstract:Model-checking for parametric stochastic models can be expressed as checking the satisfaction probability of a certain property as a function of the parameters of the model. Smoothed model checking (smMC) leverages Gaussian Processes (GP) to infer the satisfaction function over the entire parameter space from a limited set of observations obtained via simulation. This approach provides accurate reconstructions with statistically sound quantification of the uncertainty. However, it inherits the scalability issues of GP. In this paper, we exploit recent advances in probabilistic machine learning to push this limitation forward, making Bayesian inference of smMC scalable to larger datasets, enabling its application to larger models in terms of the dimension of the parameter set. We propose Stochastic Variational Smoothed Model Checking (SV-smMC), a solution that exploits stochastic variational inference (SVI) to approximate the posterior distribution of the smMC problem. The strength and flexibility of SVI make SV-smMC applicable to two alternative probabilistic models: Gaussian Processes (GP) and Bayesian Neural Networks (BNN). Moreover, SVI makes inference easily parallelizable and it enables GPU acceleration. In this paper, we compare the performances of smMC against those of SV-smMC by looking at the scalability, the computational efficiency and at the accuracy of the reconstructed satisfaction function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge