Safety Guarantees for Planning Based on Iterative Gaussian Processes
Paper and Code
Jan 17, 2020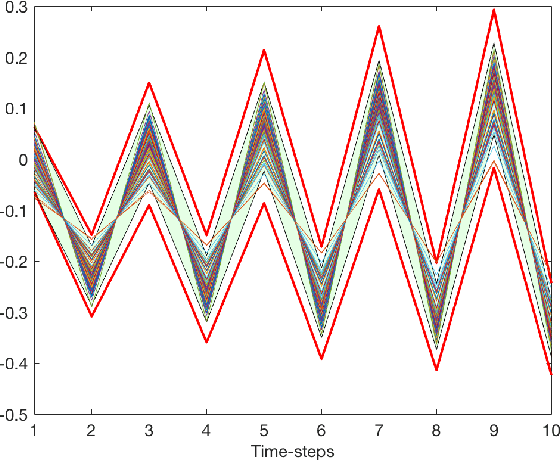
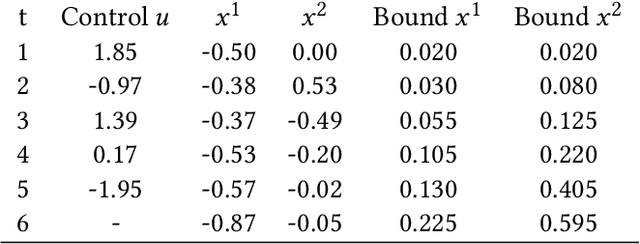
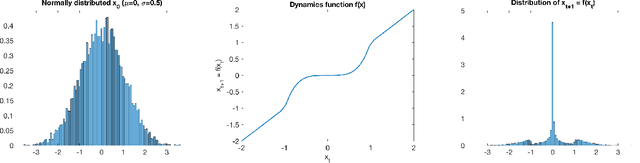
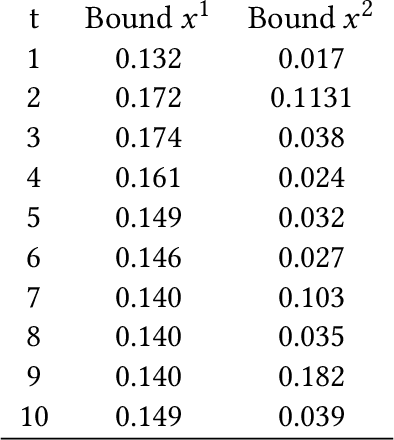
Gaussian Processes (GPs) are widely employed in control and learning because of their principled treatment of uncertainty. However, tracking uncertainty for iterative, multi-step predictions in general leads to an analytically intractable problem. While approximation methods exist, they do not come with guarantees, making it difficult to estimate their reliability and to trust their predictions. In this work, we derive formal probability error bounds for iterative prediction and planning with GPs. Building on GP properties, we bound the probability that random trajectories lie in specific regions around the predicted values. Namely, given a tolerance $\epsilon > 0 $, we compute regions around the predicted trajectory values, such that GP trajectories are guaranteed to lie inside them with probability at least $1-\epsilon$. We verify experimentally that our method tracks the predictive uncertainty correctly, even when current approximation techniques fail. Furthermore, we show how the proposed bounds can be employed within a safe reinforcement learning framework to verify the safety of candidate control policies, guiding the synthesis of provably safe controllers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge