BNN-DP: Robustness Certification of Bayesian Neural Networks via Dynamic Programming
Paper and Code
Jun 19, 2023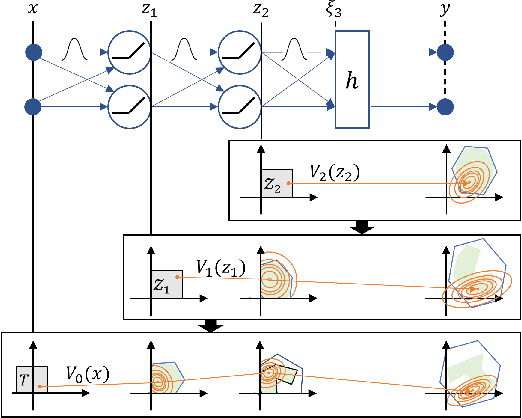
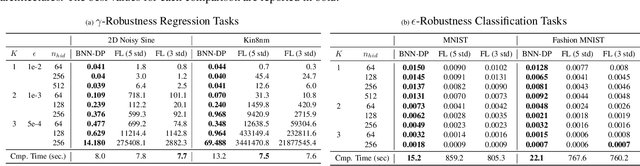
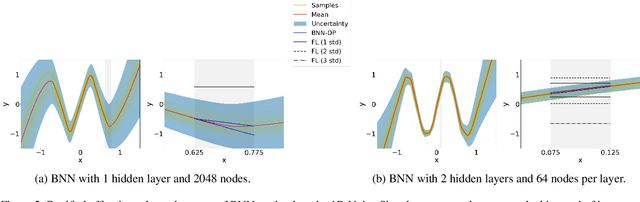
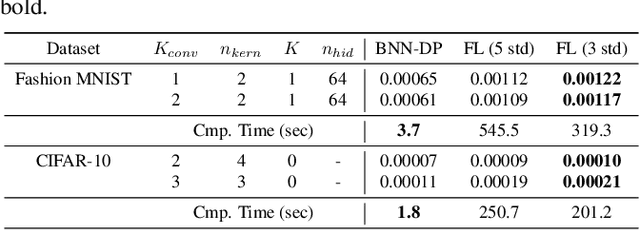
In this paper, we introduce BNN-DP, an efficient algorithmic framework for analysis of adversarial robustness of Bayesian Neural Networks (BNNs). Given a compact set of input points $T\subset \mathbb{R}^n$, BNN-DP computes lower and upper bounds on the BNN's predictions for all the points in $T$. The framework is based on an interpretation of BNNs as stochastic dynamical systems, which enables the use of Dynamic Programming (DP) algorithms to bound the prediction range along the layers of the network. Specifically, the method uses bound propagation techniques and convex relaxations to derive a backward recursion procedure to over-approximate the prediction range of the BNN with piecewise affine functions. The algorithm is general and can handle both regression and classification tasks. On a set of experiments on various regression and classification tasks and BNN architectures, we show that BNN-DP outperforms state-of-the-art methods by up to four orders of magnitude in both tightness of the bounds and computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge