FlowQ: Energy-Guided Flow Policies for Offline Reinforcement Learning

The use of guidance to steer sampling toward desired outcomes has been widely explored within diffusion models, especially in applications such as image and trajectory generation. However, incorporating guidance during training remains relatively underexplored. In this work, we introduce energy-guided flow matching, a novel approach that enhances the training of flow models and eliminates the need for guidance at inference time. We learn a conditional velocity field corresponding to the flow policy by approximating an energy-guided probability path as a Gaussian path. Learning guided trajectories is appealing for tasks where the target distribution is defined by a combination of data and an energy function, as in reinforcement learning. Diffusion-based policies have recently attracted attention for their expressive power and ability to capture multi-modal action distributions. Typically, these policies are optimized using weighted objectives or by back-propagating gradients through actions sampled by the policy. As an alternative, we propose FlowQ, an offline reinforcement learning algorithm based on energy-guided flow matching. Our method achieves competitive performance while the policy training time is constant in the number of flow sampling steps.

Guided Decoding for Robot Motion Generation and Adaption

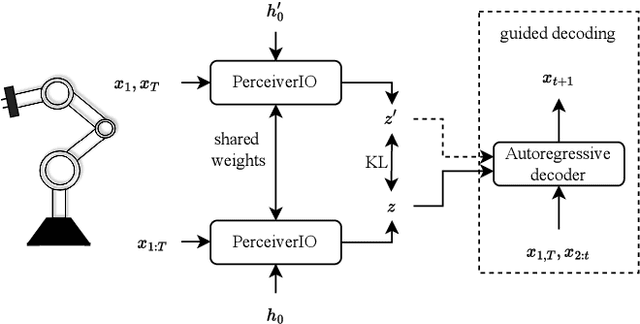
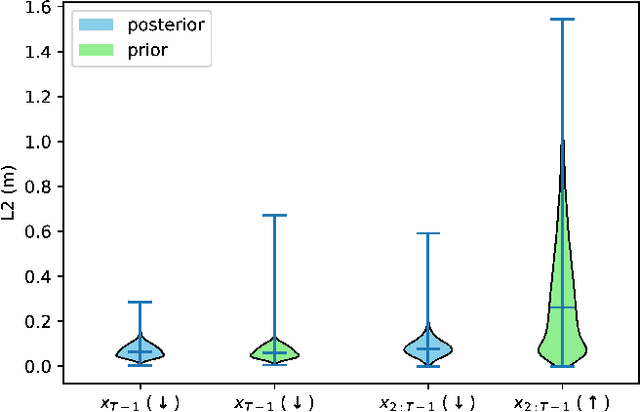
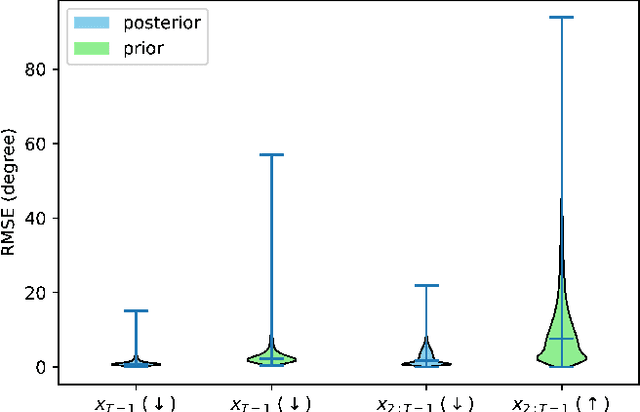
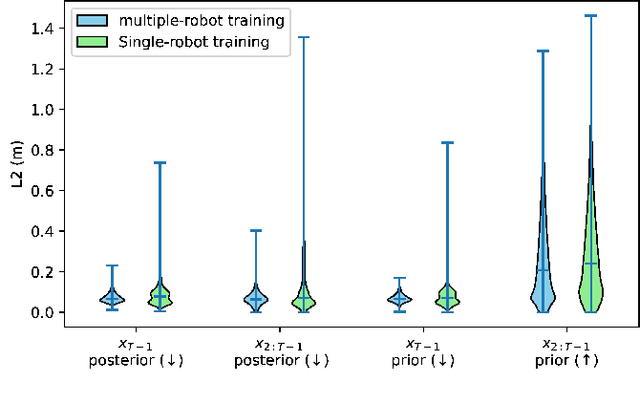
We address motion generation for high-DoF robot arms in complex settings with obstacles, via points, etc. A significant advancement in this domain is achieved by integrating Learning from Demonstration (LfD) into the motion generation process. This integration facilitates rapid adaptation to new tasks and optimizes the utilization of accumulated expertise by allowing robots to learn and generalize from demonstrated trajectories. We train a transformer architecture on a large dataset of simulated trajectories. This architecture, based on a conditional variational autoencoder transformer, learns essential motion generation skills and adapts these to meet auxiliary tasks and constraints. Our auto-regressive approach enables real-time integration of feedback from the physical system, enhancing the adaptability and efficiency of motion generation. We show that our model can generate motion from initial and target points, but also that it can adapt trajectories in navigating complex tasks, including obstacle avoidance, via points, and meeting velocity and acceleration constraints, across platforms.

Local distance preserving auto-encoders using Continuous k-Nearest Neighbours graphs

Auto-encoder models that preserve similarities in the data are a popular tool in representation learning. In this paper we introduce several auto-encoder models that preserve local distances when mapping from the data space to the latent space. We use a local distance preserving loss that is based on the continuous k-nearest neighbours graph which is known to capture topological features at all scales simultaneously. To improve training performance, we formulate learning as a constraint optimisation problem with local distance preservation as the main objective and reconstruction accuracy as a constraint. We generalise this approach to hierarchical variational auto-encoders thus learning generative models with geometrically consistent latent and data spaces. Our method provides state-of-the-art performance across several standard datasets and evaluation metrics.

Constrained Probabilistic Movement Primitives for Robot Trajectory Adaptation

Versatile movement representations allow robots to learn new tasks and rapidly adapt them to environmental changes, e.g. introduction of obstacles, placing additional robots in the workspace, modification of the joint range due to faults or range of motion constraints due to tool manipulation. Probabilistic movement primitives (ProMP) model robot movements as a distribution over trajectories and they are an important tool due to their analytical tractability and ability to learn and generalise from a small number of demonstrations. Current approaches solve specific adaptation problems, e.g. obstacle avoidance, however, a generic probabilistic approach to adaptation has not yet been developed. In this paper we propose a generic probabilistic framework for adapting ProMPs. We formulate adaptation as a constrained optimisation problem where we minimise the Kullback-Leibler divergence between the adapted distribution and the distribution of the original primitive and we constrain the probability mass associated with undesired trajectories to be low. We derive several types of constraints that can be added depending on the task, such us joint limiting, various types of obstacle avoidance, via-points, and mutual avoidance, under a common framework. We demonstrate our approach on several adaptation problems on simulated planar robot arms and 7-DOF Franka-Emika robots in single and dual robot arm settings.

Increasing the Generalisation Capacity of Conditional VAEs

We address the problem of one-to-many mappings in supervised learning, where a single instance has many different solutions of possibly equal cost. The framework of conditional variational autoencoders describes a class of methods to tackle such structured-prediction tasks by means of latent variables. We propose to incentivise informative latent representations for increasing the generalisation capacity of conditional variational autoencoders. To this end, we modify the latent variable model by defining the likelihood as a function of the latent variable only and introduce an expressive multimodal prior to enable the model for capturing semantically meaningful features of the data. To validate our approach, we train our model on the Cornell Robot Grasping dataset, and modified versions of MNIST and Fashion-MNIST obtaining results that show a significantly higher generalisation capability.

Learning Hierarchical Priors in VAEs

We propose to learn a hierarchical prior in the context of variational autoencoders to avoid the over-regularisation resulting from a standard normal prior distribution. To incentivise an informative latent representation of the data by learning a rich hierarchical prior, we formulate the objective function as the Lagrangian of a constrained-optimisation problem and propose an optimisation algorithm inspired by Taming VAEs. We introduce a graph-based interpolation method, which shows that the topology of the learned latent representation corresponds to the topology of the data manifold---and present several examples, where desired properties of latent representation such as smoothness and simple explanatory factors are learned by the prior. Furthermore, we validate our approach on standard datasets, obtaining state-of-the-art test log-likelihoods.

Efficient Low-Order Approximation of First-Passage Time Distributions

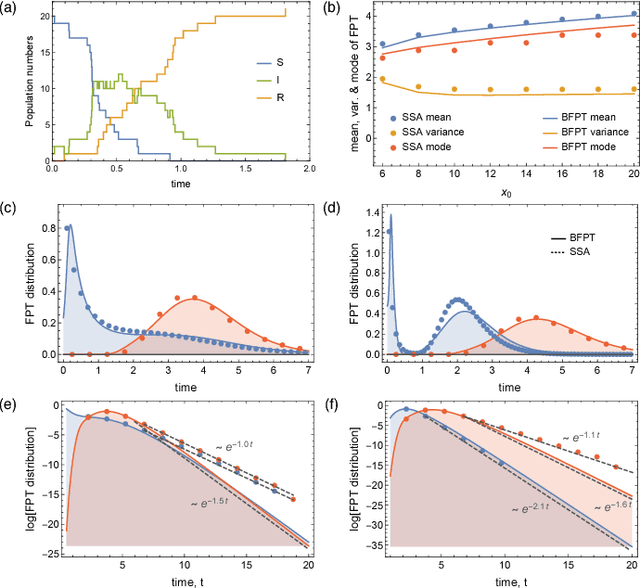
We consider the problem of computing first-passage time distributions for reaction processes modelled by master equations. We show that this generally intractable class of problems is equivalent to a sequential Bayesian inference problem for an auxiliary observation process. The solution can be approximated efficiently by solving a closed set of coupled ordinary differential equations (for the low-order moments of the process) whose size scales with the number of species. We apply it to an epidemic model and a trimerisation process, and show good agreement with stochastic simulations.

Expectation propagation for continuous time stochastic processes

We consider the inverse problem of reconstructing the posterior measure over the trajec- tories of a diffusion process from discrete time observations and continuous time constraints. We cast the problem in a Bayesian framework and derive approximations to the posterior distributions of single time marginals using variational approximate inference. We then show how the approximation can be extended to a wide class of discrete-state Markov jump pro- cesses by making use of the chemical Langevin equation. Our empirical results show that the proposed method is computationally efficient and provides good approximations for these classes of inverse problems.

f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization

Generative neural samplers are probabilistic models that implement sampling using feedforward neural networks: they take a random input vector and produce a sample from a probability distribution defined by the network weights. These models are expressive and allow efficient computation of samples and derivatives, but cannot be used for computing likelihoods or for marginalization. The generative-adversarial training method allows to train such models through the use of an auxiliary discriminative neural network. We show that the generative-adversarial approach is a special case of an existing more general variational divergence estimation approach. We show that any f-divergence can be used for training generative neural samplers. We discuss the benefits of various choices of divergence functions on training complexity and the quality of the obtained generative models.

Sparse Approximate Inference for Spatio-Temporal Point Process Models

Spatio-temporal point process models play a central role in the analysis of spatially distributed systems in several disciplines. Yet, scalable inference remains computa- tionally challenging both due to the high resolution modelling generally required and the analytically intractable likelihood function. Here, we exploit the sparsity structure typical of (spatially) discretised log-Gaussian Cox process models by using approximate message-passing algorithms. The proposed algorithms scale well with the state dimension and the length of the temporal horizon with moderate loss in distributional accuracy. They hence provide a flexible and faster alternative to both non-linear filtering-smoothing type algorithms and to approaches that implement the Laplace method or expectation propagation on (block) sparse latent Gaussian models. We infer the parameters of the latent Gaussian model using a structured variational Bayes approach. We demonstrate the proposed framework on simulation studies with both Gaussian and point-process observations and use it to reconstruct the conflict intensity and dynamics in Afghanistan from the WikiLeaks Afghan War Diary.