BALI: Learning Neural Networks via Bayesian Layerwise Inference

We introduce a new method for learning Bayesian neural networks, treating them as a stack of multivariate Bayesian linear regression models. The main idea is to infer the layerwise posterior exactly if we know the target outputs of each layer. We define these pseudo-targets as the layer outputs from the forward pass, updated by the backpropagated gradients of the objective function. The resulting layerwise posterior is a matrix-normal distribution with a Kronecker-factorized covariance matrix, which can be efficiently inverted. Our method extends to the stochastic mini-batch setting using an exponential moving average over natural-parameter terms, thus gradually forgetting older data. The method converges in few iterations and performs as well as or better than leading Bayesian neural network methods on various regression, classification, and out-of-distribution detection benchmarks.

On the detrimental effect of invariances in the likelihood for variational inference

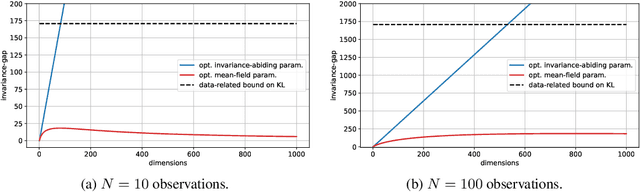
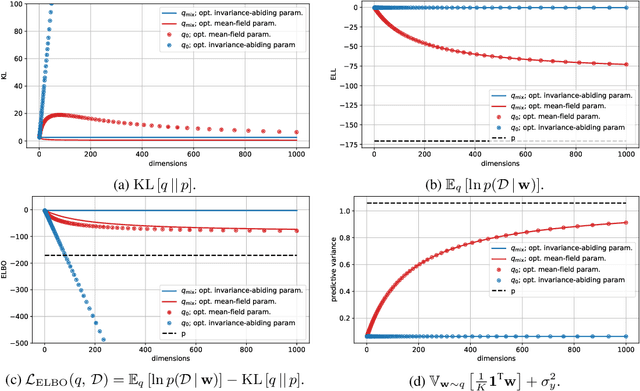
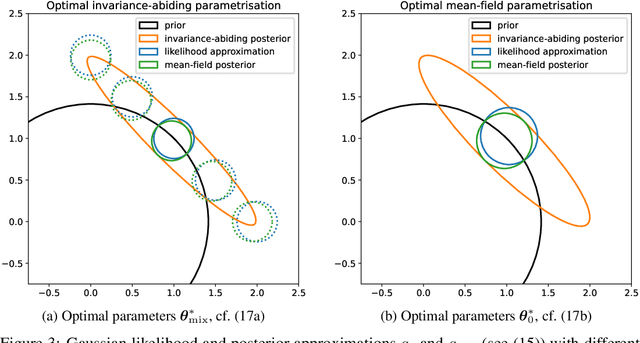
Variational Bayesian posterior inference often requires simplifying approximations such as mean-field parametrisation to ensure tractability. However, prior work has associated the variational mean-field approximation for Bayesian neural networks with underfitting in the case of small datasets or large model sizes. In this work, we show that invariances in the likelihood function of over-parametrised models contribute to this phenomenon because these invariances complicate the structure of the posterior by introducing discrete and/or continuous modes which cannot be well approximated by Gaussian mean-field distributions. In particular, we show that the mean-field approximation has an additional gap in the evidence lower bound compared to a purpose-built posterior that takes into account the known invariances. Importantly, this invariance gap is not constant; it vanishes as the approximation reverts to the prior. We proceed by first considering translation invariances in a linear model with a single data point in detail. We show that, while the true posterior can be constructed from a mean-field parametrisation, this is achieved only if the objective function takes into account the invariance gap. Then, we transfer our analysis of the linear model to neural networks. Our analysis provides a framework for future work to explore solutions to the invariance problem.

Intrinsic Anomaly Detection for Multi-Variate Time Series

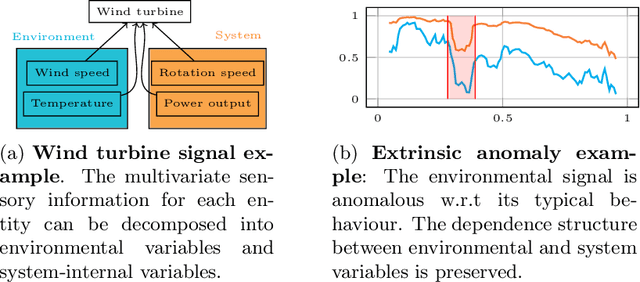
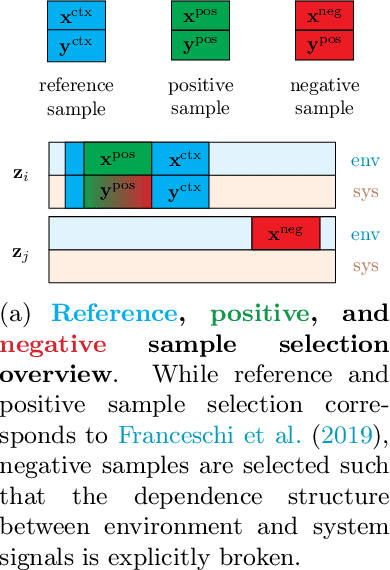
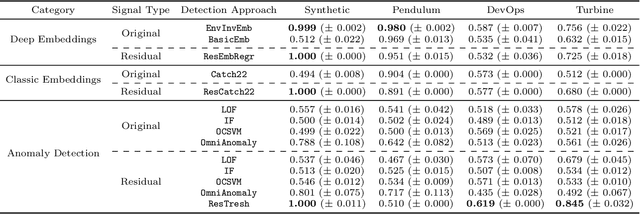
We introduce a novel, practically relevant variation of the anomaly detection problem in multi-variate time series: intrinsic anomaly detection. It appears in diverse practical scenarios ranging from DevOps to IoT, where we want to recognize failures of a system that operates under the influence of a surrounding environment. Intrinsic anomalies are changes in the functional dependency structure between time series that represent an environment and time series that represent the internal state of a system that is placed in said environment. We formalize this problem, provide under-studied public and new purpose-built data sets for it, and present methods that handle intrinsic anomaly detection. These address the short-coming of existing anomaly detection methods that cannot differentiate between expected changes in the system's state and unexpected ones, i.e., changes in the system that deviate from the environment's influence. Our most promising approach is fully unsupervised and combines adversarial learning and time series representation learning, thereby addressing problems such as label sparsity and subjectivity, while allowing to navigate and improve notoriously problematic anomaly detection data sets.

Deep Explicit Duration Switching Models for Time Series

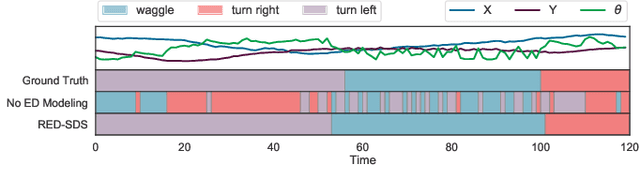
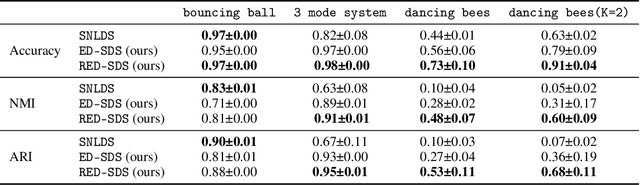
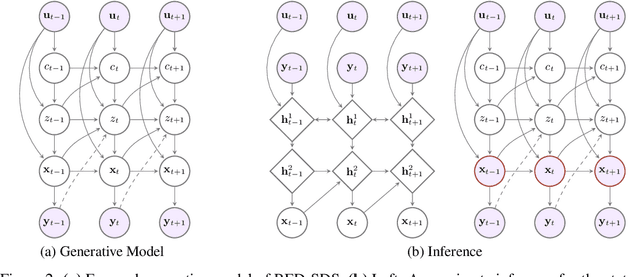
Many complex time series can be effectively subdivided into distinct regimes that exhibit persistent dynamics. Discovering the switching behavior and the statistical patterns in these regimes is important for understanding the underlying dynamical system. We propose the Recurrent Explicit Duration Switching Dynamical System (RED-SDS), a flexible model that is capable of identifying both state- and time-dependent switching dynamics. State-dependent switching is enabled by a recurrent state-to-switch connection and an explicit duration count variable is used to improve the time-dependent switching behavior. We demonstrate how to perform efficient inference using a hybrid algorithm that approximates the posterior of the continuous states via an inference network and performs exact inference for the discrete switches and counts. The model is trained by maximizing a Monte Carlo lower bound of the marginal log-likelihood that can be computed efficiently as a byproduct of the inference routine. Empirical results on multiple datasets demonstrate that RED-SDS achieves considerable improvement in time series segmentation and competitive forecasting performance against the state of the art.

Learning Hierarchical Priors in VAEs

We propose to learn a hierarchical prior in the context of variational autoencoders to avoid the over-regularisation resulting from a standard normal prior distribution. To incentivise an informative latent representation of the data by learning a rich hierarchical prior, we formulate the objective function as the Lagrangian of a constrained-optimisation problem and propose an optimisation algorithm inspired by Taming VAEs. We introduce a graph-based interpolation method, which shows that the topology of the learned latent representation corresponds to the topology of the data manifold---and present several examples, where desired properties of latent representation such as smoothness and simple explanatory factors are learned by the prior. Furthermore, we validate our approach on standard datasets, obtaining state-of-the-art test log-likelihoods.

Multi-Source Neural Variational Inference

Learning from multiple sources of information is an important problem in machine-learning research. The key challenges are learning representations and formulating inference methods that take into account the complementarity and redundancy of various information sources. In this paper we formulate a variational autoencoder based multi-source learning framework in which each encoder is conditioned on a different information source. This allows us to relate the sources via the shared latent variables by computing divergence measures between individual source's posterior approximations. We explore a variety of options to learn these encoders and to integrate the beliefs they compute into a consistent posterior approximation. We visualise learned beliefs on a toy dataset and evaluate our methods for learning shared representations and structured output prediction, showing trade-offs of learning separate encoders for each information source. Furthermore, we demonstrate how conflict detection and redundancy can increase robustness of inference in a multi-source setting.

Metrics for Deep Generative Models

Neural samplers such as variational autoencoders (VAEs) or generative adversarial networks (GANs) approximate distributions by transforming samples from a simple random source---the latent space---to samples from a more complex distribution represented by a dataset. While the manifold hypothesis implies that the density induced by a dataset contains large regions of low density, the training criterions of VAEs and GANs will make the latent space densely covered. Consequently points that are separated by low-density regions in observation space will be pushed together in latent space, making stationary distances poor proxies for similarity. We transfer ideas from Riemannian geometry to this setting, letting the distance between two points be the shortest path on a Riemannian manifold induced by the transformation. The method yields a principled distance measure, provides a tool for visual inspection of deep generative models, and an alternative to linear interpolation in latent space. In addition, it can be applied for robot movement generalization using previously learned skills. The method is evaluated on a synthetic dataset with known ground truth; on a simulated robot arm dataset; on human motion capture data; and on a generative model of handwritten digits.