Deep Explicit Duration Switching Models for Time Series
Paper and Code
Oct 26, 2021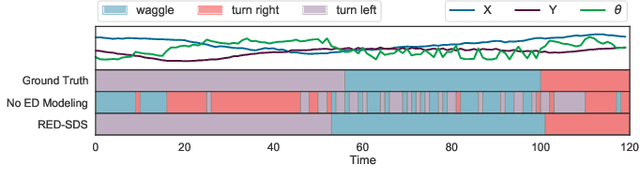
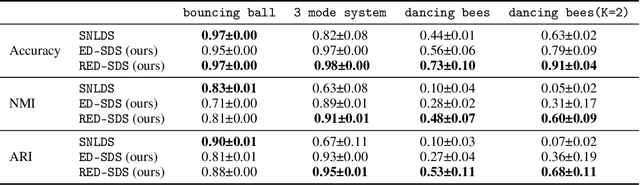
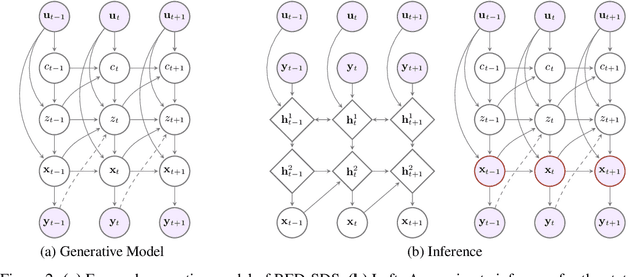

Many complex time series can be effectively subdivided into distinct regimes that exhibit persistent dynamics. Discovering the switching behavior and the statistical patterns in these regimes is important for understanding the underlying dynamical system. We propose the Recurrent Explicit Duration Switching Dynamical System (RED-SDS), a flexible model that is capable of identifying both state- and time-dependent switching dynamics. State-dependent switching is enabled by a recurrent state-to-switch connection and an explicit duration count variable is used to improve the time-dependent switching behavior. We demonstrate how to perform efficient inference using a hybrid algorithm that approximates the posterior of the continuous states via an inference network and performs exact inference for the discrete switches and counts. The model is trained by maximizing a Monte Carlo lower bound of the marginal log-likelihood that can be computed efficiently as a byproduct of the inference routine. Empirical results on multiple datasets demonstrate that RED-SDS achieves considerable improvement in time series segmentation and competitive forecasting performance against the state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge