BALI: Learning Neural Networks via Bayesian Layerwise Inference

We introduce a new method for learning Bayesian neural networks, treating them as a stack of multivariate Bayesian linear regression models. The main idea is to infer the layerwise posterior exactly if we know the target outputs of each layer. We define these pseudo-targets as the layer outputs from the forward pass, updated by the backpropagated gradients of the objective function. The resulting layerwise posterior is a matrix-normal distribution with a Kronecker-factorized covariance matrix, which can be efficiently inverted. Our method extends to the stochastic mini-batch setting using an exponential moving average over natural-parameter terms, thus gradually forgetting older data. The method converges in few iterations and performs as well as or better than leading Bayesian neural network methods on various regression, classification, and out-of-distribution detection benchmarks.

Learning Flat Latent Manifolds with VAEs

Measuring the similarity between data points often requires domain knowledge. This can in parts be compensated by relying on unsupervised methods such as latent-variable models, where similarity/distance is estimated in a more compact latent space. Prevalent is the use of the Euclidean metric, which has the drawback of ignoring information about similarity of data stored in the decoder, as captured by the framework of Riemannian geometry. Alternatives---such as approximating the geodesic---are often computationally inefficient, rendering the methods impractical. We propose an extension to the framework of variational auto-encoders allows learning flat latent manifolds, where the Euclidean metric is a proxy for the similarity between data points. This is achieved by defining the latent space as a Riemannian manifold and by regularising the metric tensor to be a scaled identity matrix. Additionally, we replace the compact prior typically used in variational auto-encoders with a recently presented, more expressive hierarchical one---and formulate the learning problem as a constrained optimisation problem. We evaluate our method on a range of data-sets, including a video-tracking benchmark, where the performance of our unsupervised approach nears that of state-of-the-art supervised approaches, while retaining the computational efficiency of straight-line-based approaches.

Increasing the Generalisation Capacity of Conditional VAEs

We address the problem of one-to-many mappings in supervised learning, where a single instance has many different solutions of possibly equal cost. The framework of conditional variational autoencoders describes a class of methods to tackle such structured-prediction tasks by means of latent variables. We propose to incentivise informative latent representations for increasing the generalisation capacity of conditional variational autoencoders. To this end, we modify the latent variable model by defining the likelihood as a function of the latent variable only and introduce an expressive multimodal prior to enable the model for capturing semantically meaningful features of the data. To validate our approach, we train our model on the Cornell Robot Grasping dataset, and modified versions of MNIST and Fashion-MNIST obtaining results that show a significantly higher generalisation capability.

Learning Hierarchical Priors in VAEs

We propose to learn a hierarchical prior in the context of variational autoencoders to avoid the over-regularisation resulting from a standard normal prior distribution. To incentivise an informative latent representation of the data by learning a rich hierarchical prior, we formulate the objective function as the Lagrangian of a constrained-optimisation problem and propose an optimisation algorithm inspired by Taming VAEs. We introduce a graph-based interpolation method, which shows that the topology of the learned latent representation corresponds to the topology of the data manifold---and present several examples, where desired properties of latent representation such as smoothness and simple explanatory factors are learned by the prior. Furthermore, we validate our approach on standard datasets, obtaining state-of-the-art test log-likelihoods.

Fast Approximate Geodesics for Deep Generative Models

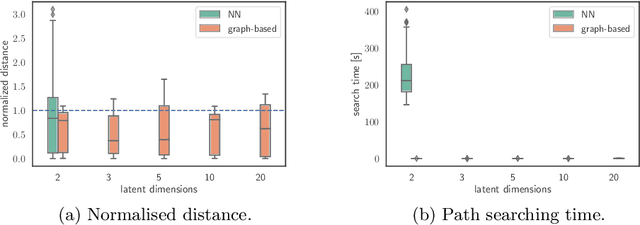
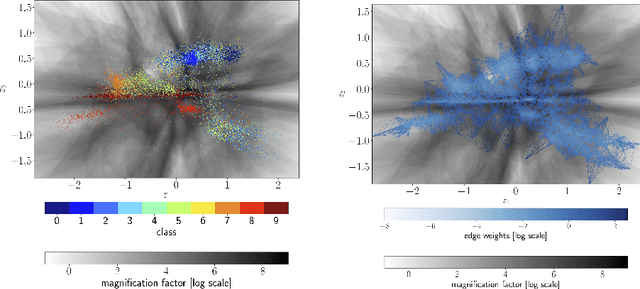
The length of the geodesic between two data points along the Riemannian manifold, induced by a deep generative model, yields a principled measure of similarity. Applications have so far been limited to low-dimensional latent spaces, as the method is computationally demanding: it constitutes to solving a non-convex optimisation problem. Our approach is to tackle a relaxation: finding shortest paths in a finite graph of samples from the aggregate approximate posterior can be solved exactly, at greatly reduced runtime, and without notable loss in quality. The method is hence applicable to high-dimensional problems in the visual domain. We validate the approach empirically on a series of experiments using variational autoencoders applied to image data, tackling the Chair, Faces and FashionMNIST data sets.

Active Learning based on Data Uncertainty and Model Sensitivity

Robots can rapidly acquire new skills from demonstrations. However, during generalisation of skills or transitioning across fundamentally different skills, it is unclear whether the robot has the necessary knowledge to perform the task. Failing to detect missing information often leads to abrupt movements or to collisions with the environment. Active learning can quantify the uncertainty of performing the task and, in general, locate regions of missing information. We introduce a novel algorithm for active learning and demonstrate its utility for generating smooth trajectories. Our approach is based on deep generative models and metric learning in latent spaces. It relies on the Jacobian of the likelihood to detect non-smooth transitions in the latent space, i.e., transitions that lead to abrupt changes in the movement of the robot. When non-smooth transitions are detected, our algorithm asks for an additional demonstration from that specific region. The newly acquired knowledge modifies the data manifold and allows for learning a latent representation for generating smooth movements. We demonstrate the efficacy of our approach on generalising elementary skills, transitioning across different skills, and implicitly avoiding collisions with the environment. For our experiments, we use a simulated pendulum where we observe its motion from images and a 7-DoF anthropomorphic arm.

Metrics for Deep Generative Models

Neural samplers such as variational autoencoders (VAEs) or generative adversarial networks (GANs) approximate distributions by transforming samples from a simple random source---the latent space---to samples from a more complex distribution represented by a dataset. While the manifold hypothesis implies that the density induced by a dataset contains large regions of low density, the training criterions of VAEs and GANs will make the latent space densely covered. Consequently points that are separated by low-density regions in observation space will be pushed together in latent space, making stationary distances poor proxies for similarity. We transfer ideas from Riemannian geometry to this setting, letting the distance between two points be the shortest path on a Riemannian manifold induced by the transformation. The method yields a principled distance measure, provides a tool for visual inspection of deep generative models, and an alternative to linear interpolation in latent space. In addition, it can be applied for robot movement generalization using previously learned skills. The method is evaluated on a synthetic dataset with known ground truth; on a simulated robot arm dataset; on human motion capture data; and on a generative model of handwritten digits.