Process-aware Human Activity Recognition

Humans naturally follow distinct patterns when conducting their daily activities, which are driven by established practices and processes, such as production workflows, social norms and daily routines. Human activity recognition (HAR) algorithms usually use neural networks or machine learning techniques to analyse inherent relationships within the data. However, these approaches often overlook the contextual information in which the data are generated, potentially limiting their effectiveness. We propose a novel approach that incorporates process information from context to enhance the HAR performance. Specifically, we align probabilistic events generated by machine learning models with process models derived from contextual information. This alignment adaptively weighs these two sources of information to optimise HAR accuracy. Our experiments demonstrate that our approach achieves better accuracy and Macro F1-score compared to baseline models.

Active and sparse methods in smoothed model checking

Smoothed model checking based on Gaussian process classification provides a powerful approach for statistical model checking of parametric continuous time Markov chain models. The method constructs a model for the functional dependence of satisfaction probability on the Markov chain parameters. This is done via Gaussian process inference methods from a limited number of observations for different parameter combinations. In this work we consider extensions to smoothed model checking based on sparse variational methods and active learning. Both are used successfully to improve the scalability of smoothed model checking. In particular, we see that active learning-based ideas for iteratively querying the simulation model for observations can be used to steer the model-checking to more informative areas of the parameter space and thus improve sample efficiency. Online extensions of sparse variational Gaussian process inference algorithms are demonstrated to provide a scalable method for implementing active learning approaches for smoothed model checking.

Experiential AI

Experiential AI is proposed as a new research agenda in which artists and scientists come together to dispel the mystery of algorithms and make their mechanisms vividly apparent. It addresses the challenge of finding novel ways of opening up the field of artificial intelligence to greater transparency and collaboration between human and machine. The hypothesis is that art can mediate between computer code and human comprehension to overcome the limitations of explanations in and for AI systems. Artists can make the boundaries of systems visible and offer novel ways to make the reasoning of AI transparent and decipherable. Beyond this, artistic practice can explore new configurations of humans and algorithms, mapping the terrain of inter-agencies between people and machines. This helps to viscerally understand the complex causal chains in environments with AI components, including questions about what data to collect or who to collect it about, how the algorithms are chosen, commissioned and configured or how humans are conditioned by their participation in algorithmic processes.

Geometric fluid approximation for general continuous-time Markov chains

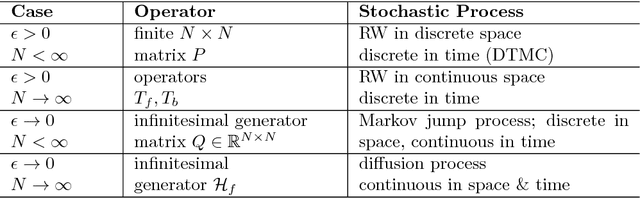
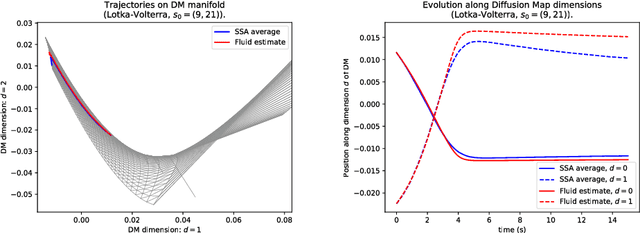
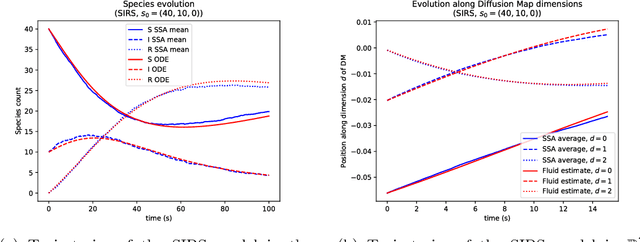
Fluid approximations have seen great success in approximating the macro-scale behaviour of Markov systems with a large number of discrete states. However, these methods rely on the continuous-time Markov chain (CTMC) having a particular population structure which suggests a natural continuous state-space endowed with a dynamics for the approximating process. We construct here a general method based on spectral analysis of the transition matrix of the CTMC, without the need for a population structure. Specifically, we use the popular manifold learning method of diffusion maps to analyse the transition matrix as the operator of a hidden continuous process. An embedding of states in a continuous space is recovered, and the space is endowed with a drift vector field inferred via Gaussian process regression. In this manner, we construct an ODE whose solution approximates the evolution of the CTMC mean, mapped onto the continuous space (known as the fluid limit).

Property-driven State-Space Coarsening for Continuous Time Markov Chains

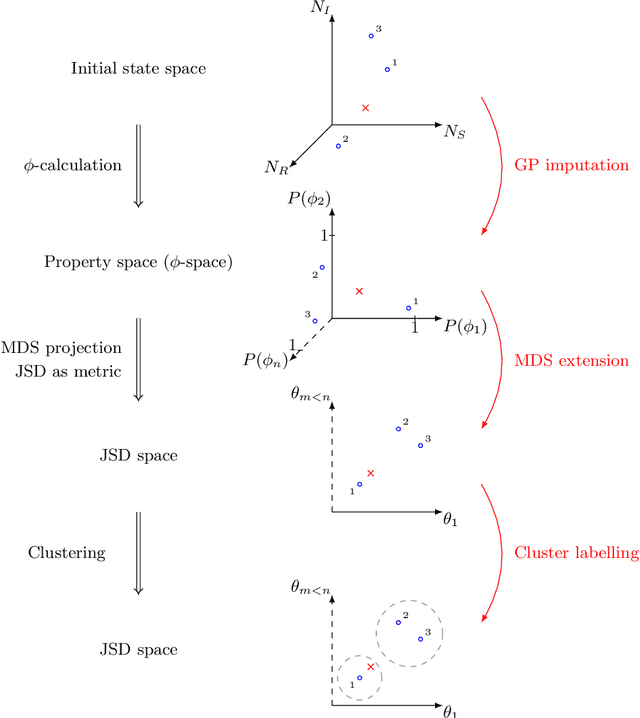
Dynamical systems with large state-spaces are often expensive to thoroughly explore experimentally. Coarse-graining methods aim to define simpler systems which are more amenable to analysis and exploration; most current methods, however, focus on a priori state aggregation based on similarities in transition rates, which is not necessarily reflected in similar behaviours at the level of trajectories. We propose a way to coarsen the state-space of a system which optimally preserves the satisfaction of a set of logical specifications about the system's trajectories. Our approach is based on Gaussian Process emulation and Multi-Dimensional Scaling, a dimensionality reduction technique which optimally preserves distances in non-Euclidean spaces. We show how to obtain low-dimensional visualisations of the system's state-space from the perspective of properties' satisfaction, and how to define macro-states which behave coherently with respect to the specifications. Our approach is illustrated on a non-trivial running example, showing promising performance and high computational efficiency.

Unbiased Bayesian Inference for Population Markov Jump Processes via Random Truncations

We consider continuous time Markovian processes where populations of individual agents interact stochastically according to kinetic rules. Despite the increasing prominence of such models in fields ranging from biology to smart cities, Bayesian inference for such systems remains challenging, as these are continuous time, discrete state systems with potentially infinite state-space. Here we propose a novel efficient algorithm for joint state / parameter posterior sampling in population Markov Jump processes. We introduce a class of pseudo-marginal sampling algorithms based on a random truncation method which enables a principled treatment of infinite state spaces. Extensive evaluation on a number of benchmark models shows that this approach achieves considerable savings compared to state of the art methods, retaining accuracy and fast convergence. We also present results on a synthetic biology data set showing the potential for practical usefulness of our work.