A Unified View of Stochastic Hamiltonian Sampling

In this work, we revisit the theoretical properties of Hamiltonian stochastic differential equations (SDEs) for Bayesian posterior sampling, and we study the two types of errors that arise from numerical SDE simulation: the discretization error and the error due to noisy gradient estimates in the context of data subsampling. We consider overlooked results describing the ergodic convergence rates of numerical integration schemes, and we produce a novel analysis for the effect of mini-batches through the lens of differential operator splitting. In our analysis, the stochastic component of the proposed Hamiltonian SDE is decoupled from the gradient noise, for which we make no normality assumptions. This allows us to derive interesting connections among different sampling schemes, including the original Hamiltonian Monte Carlo (HMC) algorithm, and explain their performance. We show that for a careful selection of numerical integrators, both errors vanish at a rate $\mathcal{O}(\eta^2)$, where $\eta$ is the integrator step size. Our theoretical results are supported by an empirical study on a variety of regression and classification tasks for Bayesian neural networks.

Model Selection for Bayesian Autoencoders

We develop a novel method for carrying out model selection for Bayesian autoencoders (BAEs) by means of prior hyper-parameter optimization. Inspired by the common practice of type-II maximum likelihood optimization and its equivalence to Kullback-Leibler divergence minimization, we propose to optimize the distributional sliced-Wasserstein distance (DSWD) between the output of the autoencoder and the empirical data distribution. The advantages of this formulation are that we can estimate the DSWD based on samples and handle high-dimensional problems. We carry out posterior estimation of the BAE parameters via stochastic gradient Hamiltonian Monte Carlo and turn our BAE into a generative model by fitting a flexible Dirichlet mixture model in the latent space. Consequently, we obtain a powerful alternative to variational autoencoders, which are the preferred choice in modern applications of autoencoders for representation learning with uncertainty. We evaluate our approach qualitatively and quantitatively using a vast experimental campaign on a number of unsupervised learning tasks and show that, in small-data regimes where priors matter, our approach provides state-of-the-art results, outperforming multiple competitive baselines.

All You Need is a Good Functional Prior for Bayesian Deep Learning

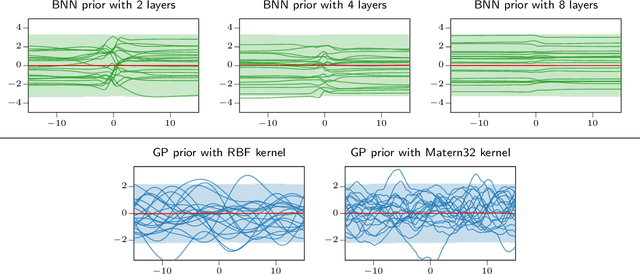
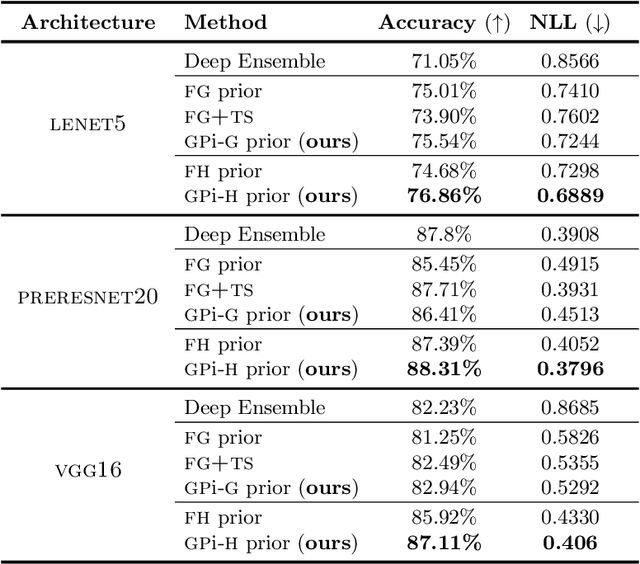
The Bayesian treatment of neural networks dictates that a prior distribution is specified over their weight and bias parameters. This poses a challenge because modern neural networks are characterized by a large number of parameters, and the choice of these priors has an uncontrolled effect on the induced functional prior, which is the distribution of the functions obtained by sampling the parameters from their prior distribution. We argue that this is a hugely limiting aspect of Bayesian deep learning, and this work tackles this limitation in a practical and effective way. Our proposal is to reason in terms of functional priors, which are easier to elicit, and to "tune" the priors of neural network parameters in a way that they reflect such functional priors. Gaussian processes offer a rigorous framework to define prior distributions over functions, and we propose a novel and robust framework to match their prior with the functional prior of neural networks based on the minimization of their Wasserstein distance. We provide vast experimental evidence that coupling these priors with scalable Markov chain Monte Carlo sampling offers systematically large performance improvements over alternative choices of priors and state-of-the-art approximate Bayesian deep learning approaches. We consider this work a considerable step in the direction of making the long-standing challenge of carrying out a fully Bayesian treatment of neural networks, including convolutional neural networks, a concrete possibility.

Sparse within Sparse Gaussian Processes using Neighbor Information

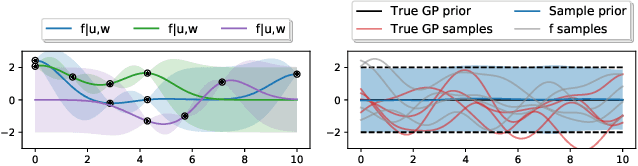
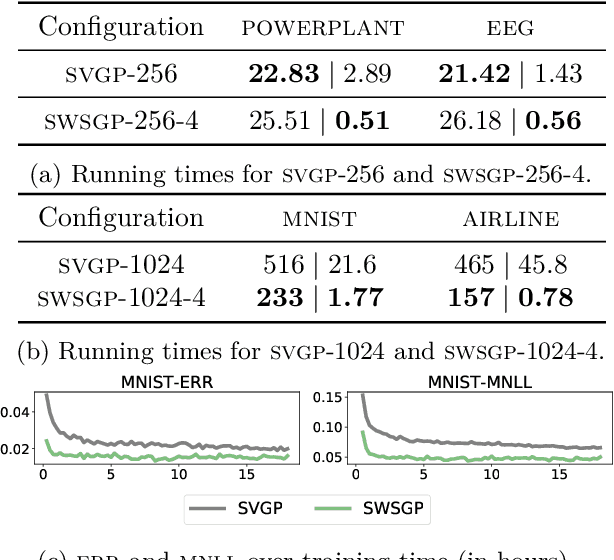
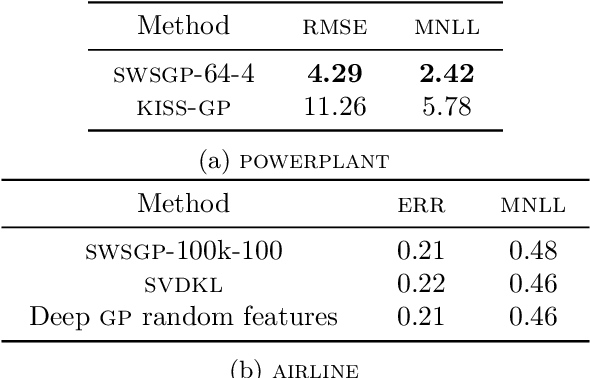
Approximations to Gaussian processes based on inducing variables, combined with variational inference techniques, enable state-of-the-art sparse approaches to infer GPs at scale through mini batch-based learning. In this work, we address one limitation of sparse GPs, which is due to the challenge in dealing with a large number of inducing variables without imposing a special structure on the inducing inputs. In particular, we introduce a novel hierarchical prior, which imposes sparsity on the set of inducing variables. We treat our model variationally, and we experimentally show considerable computational gains compared to standard sparse GPs when sparsity on the inducing variables is realized considering the nearest inducing inputs of a random mini-batch of the data. We perform an extensive experimental validation that demonstrates the effectiveness of our approach compared to the state-of-the-art. Our approach enables the possibility to use sparse GPs using a large number of inducing points without incurring a prohibitive computational cost.

Isotropic SGD: a Practical Approach to Bayesian Posterior Sampling

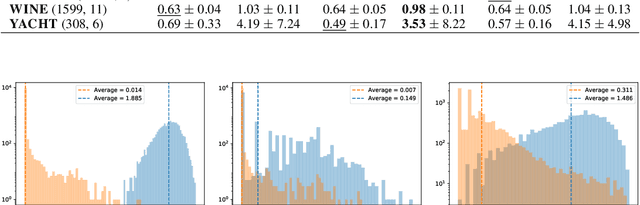
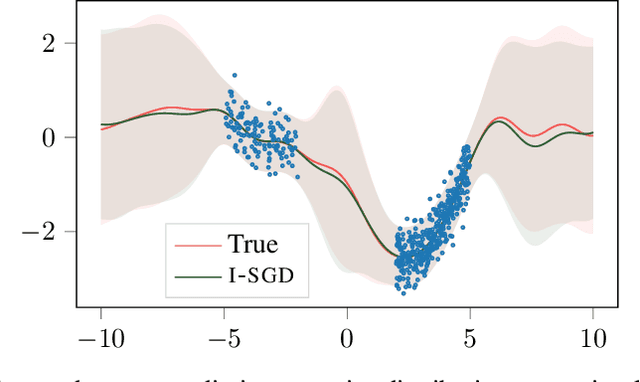
In this work we define a unified mathematical framework to deepen our understanding of the role of stochastic gradient (SG) noise on the behavior of Markov chain Monte Carlo sampling (SGMCMC) algorithms. Our formulation unlocks the design of a novel, practical approach to posterior sampling, which makes the SG noise isotropic using a fixed learning rate that we determine analytically, and that requires weaker assumptions than existing algorithms. In contrast, the common traits of existing \sgmcmc algorithms is to approximate the isotropy condition either by drowning the gradients in additive noise (annealing the learning rate) or by making restrictive assumptions on the \sg noise covariance and the geometry of the loss landscape. Extensive experimental validations indicate that our proposal is competitive with the state-of-the-art on \sgmcmc, while being much more practical to use.

A Variational View on Bootstrap Ensembles as Bayesian Inference

In this paper, we employ variational arguments to establish a connection between ensemble methods for Neural Networks and Bayesian inference. We consider an ensemble-based scheme where each model/particle corresponds to a perturbation of the data by means of parametric bootstrap and a perturbation of the prior. We derive conditions under which any optimization steps of the particles makes the associated distribution reduce its divergence to the posterior over model parameters. Such conditions do not require any particular form for the approximation and they are purely geometrical, giving insights on the behavior of the ensemble on a number of interesting models such as Neural Networks with ReLU activations. Experiments confirm that ensemble methods can be a valid alternative to approximate Bayesian inference; the theoretical developments in the paper seek to explain this behavior.

Dirichlet-based Gaussian Processes for Large-scale Calibrated Classification

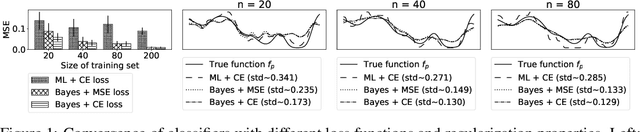
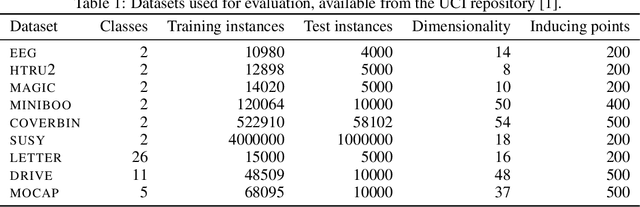
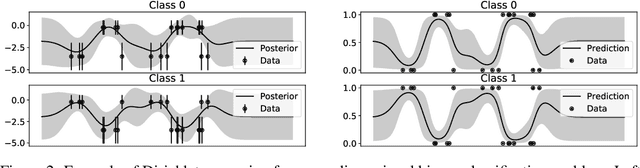
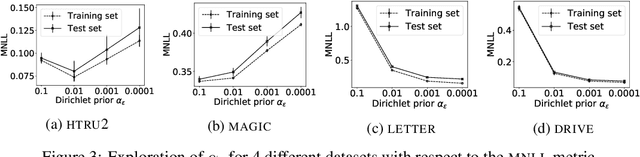
In this paper, we study the problem of deriving fast and accurate classification algorithms with uncertainty quantification. Gaussian process classification provides a principled approach, but the corresponding computational burden is hardly sustainable in large-scale problems and devising efficient alternatives is a challenge. In this work, we investigate if and how Gaussian process regression directly applied to the classification labels can be used to tackle this question. While in this case training time is remarkably faster, predictions need be calibrated for classification and uncertainty estimation. To this aim, we propose a novel approach based on interpreting the labels as the output of a Dirichlet distribution. Extensive experimental results show that the proposed approach provides essentially the same accuracy and uncertainty quantification of Gaussian process classification while requiring only a fraction of computational resources.

Property-driven State-Space Coarsening for Continuous Time Markov Chains

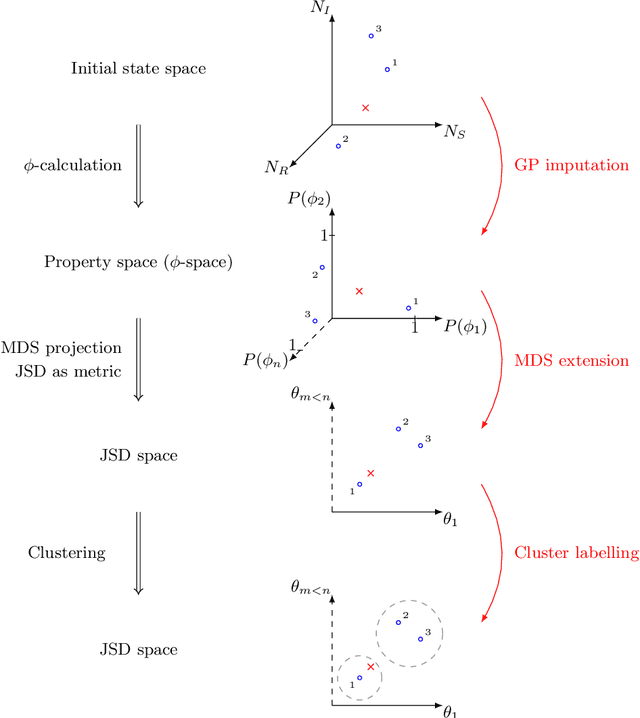
Dynamical systems with large state-spaces are often expensive to thoroughly explore experimentally. Coarse-graining methods aim to define simpler systems which are more amenable to analysis and exploration; most current methods, however, focus on a priori state aggregation based on similarities in transition rates, which is not necessarily reflected in similar behaviours at the level of trajectories. We propose a way to coarsen the state-space of a system which optimally preserves the satisfaction of a set of logical specifications about the system's trajectories. Our approach is based on Gaussian Process emulation and Multi-Dimensional Scaling, a dimensionality reduction technique which optimally preserves distances in non-Euclidean spaces. We show how to obtain low-dimensional visualisations of the system's state-space from the perspective of properties' satisfaction, and how to define macro-states which behave coherently with respect to the specifications. Our approach is illustrated on a non-trivial running example, showing promising performance and high computational efficiency.