Isotropic SGD: a Practical Approach to Bayesian Posterior Sampling

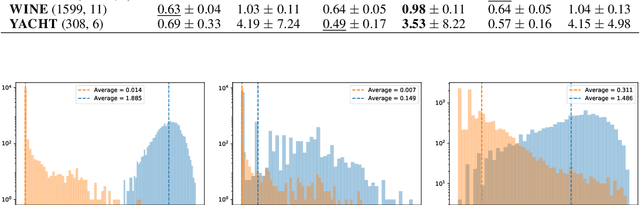
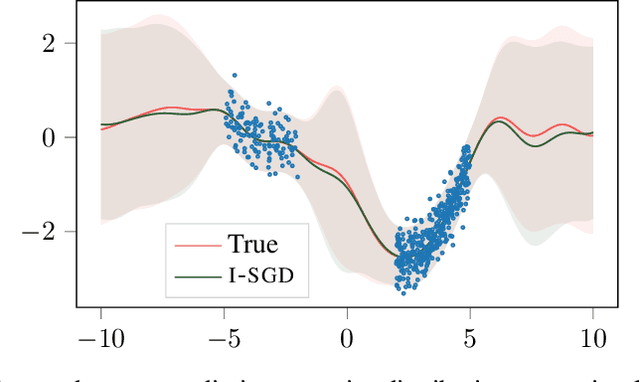
In this work we define a unified mathematical framework to deepen our understanding of the role of stochastic gradient (SG) noise on the behavior of Markov chain Monte Carlo sampling (SGMCMC) algorithms. Our formulation unlocks the design of a novel, practical approach to posterior sampling, which makes the SG noise isotropic using a fixed learning rate that we determine analytically, and that requires weaker assumptions than existing algorithms. In contrast, the common traits of existing \sgmcmc algorithms is to approximate the isotropy condition either by drowning the gradients in additive noise (annealing the learning rate) or by making restrictive assumptions on the \sg noise covariance and the geometry of the loss landscape. Extensive experimental validations indicate that our proposal is competitive with the state-of-the-art on \sgmcmc, while being much more practical to use.

Sparsification as a Remedy for Staleness in Distributed Asynchronous SGD

Large scale machine learning is increasingly relying on distributed optimization, whereby several machines contribute to the training process of a statistical model. While there exist a large literature on stochastic gradient descent (SGD) and variants, the study of countermeasures to mitigate problems arising in asynchronous distributed settings are still in their infancy. The key question of this work is whether sparsification, a technique predominantly used to reduce communication overheads, can also mitigate the staleness problem that affects asynchronous SGD. We study the role of sparsification both theoretically and empirically. Our theory indicates that, in an asynchronous, non-convex setting, the ergodic convergence rate of sparsified SGD matches the known result $\mathcal{O} \left( 1/\sqrt{T} \right)$ of non-convex SGD. We then carry out an empirical study to complement our theory and show that, in practice, sparsification consistently improves over vanilla SGD and current alternatives to mitigate the effects of staleness.