Sparse within Sparse Gaussian Processes using Neighbor Information

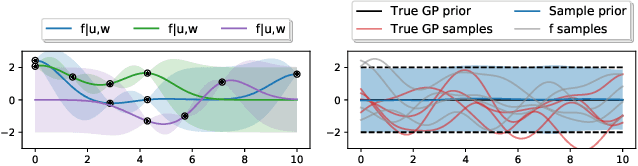
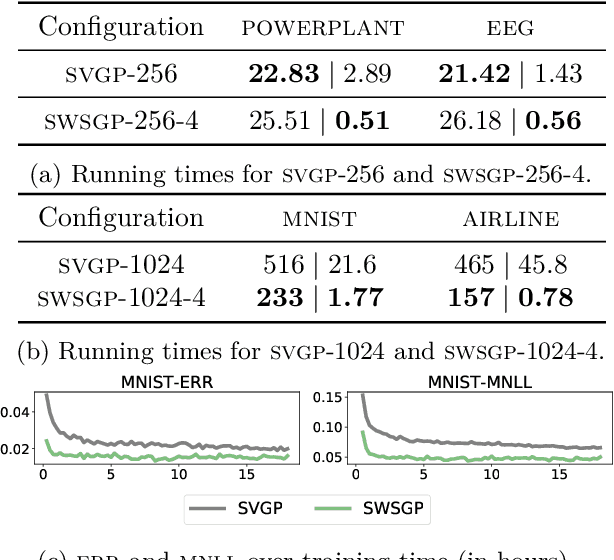
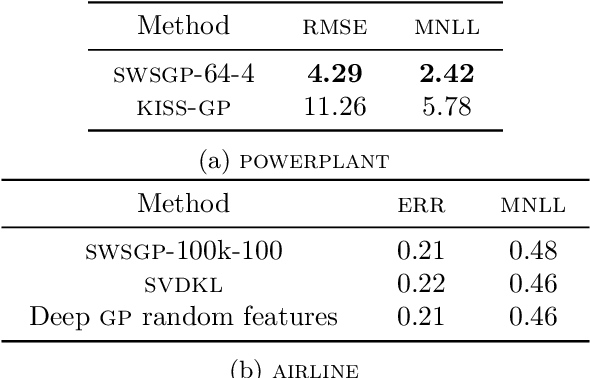
Approximations to Gaussian processes based on inducing variables, combined with variational inference techniques, enable state-of-the-art sparse approaches to infer GPs at scale through mini batch-based learning. In this work, we address one limitation of sparse GPs, which is due to the challenge in dealing with a large number of inducing variables without imposing a special structure on the inducing inputs. In particular, we introduce a novel hierarchical prior, which imposes sparsity on the set of inducing variables. We treat our model variationally, and we experimentally show considerable computational gains compared to standard sparse GPs when sparsity on the inducing variables is realized considering the nearest inducing inputs of a random mini-batch of the data. We perform an extensive experimental validation that demonstrates the effectiveness of our approach compared to the state-of-the-art. Our approach enables the possibility to use sparse GPs using a large number of inducing points without incurring a prohibitive computational cost.

Calibrating Deep Convolutional Gaussian Processes

The wide adoption of Convolutional Neural Networks (CNNs) in applications where decision-making under uncertainty is fundamental, has brought a great deal of attention to the ability of these models to accurately quantify the uncertainty in their predictions. Previous work on combining CNNs with Gaussian processes (GPs) has been developed under the assumption that the predictive probabilities of these models are well-calibrated. In this paper we show that, in fact, current combinations of CNNs and GPs are miscalibrated. We proposes a novel combination that considerably outperforms previous approaches on this aspect, while achieving state-of-the-art performance on image classification tasks.