Dynamic Policy Programming
Paper and Code
Sep 06, 2011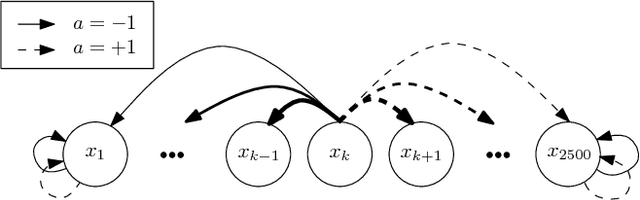
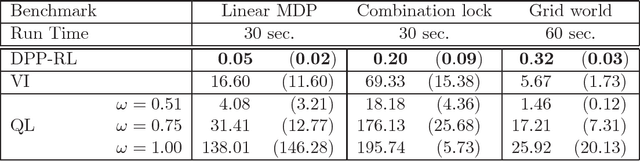
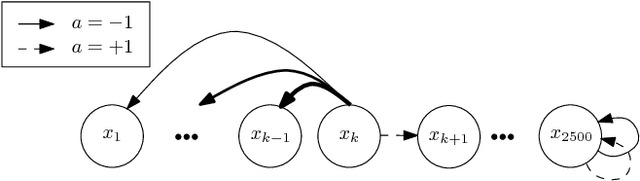

In this paper, we propose a novel policy iteration method, called dynamic policy programming (DPP), to estimate the optimal policy in the infinite-horizon Markov decision processes. We prove the finite-iteration and asymptotic l\infty-norm performance-loss bounds for DPP in the presence of approximation/estimation error. The bounds are expressed in terms of the l\infty-norm of the average accumulated error as opposed to the l\infty-norm of the error in the case of the standard approximate value iteration (AVI) and the approximate policy iteration (API). This suggests that DPP can achieve a better performance than AVI and API since it averages out the simulation noise caused by Monte-Carlo sampling throughout the learning process. We examine this theoretical results numerically by com- paring the performance of the approximate variants of DPP with existing reinforcement learning (RL) methods on different problem domains. Our results show that, in all cases, DPP-based algorithms outperform other RL methods by a wide margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge