Approximate inference on planar graphs using Loop Calculus and Belief Propagation

We introduce novel results for approximate inference on planar graphical models using the loop calculus framework. The loop calculus (Chertkov and Chernyak, 2006b) allows to express the exact partition function Z of a graphical model as a finite sum of terms that can be evaluated once the belief propagation (BP) solution is known. In general, full summation over all correction terms is intractable. We develop an algorithm for the approach presented in Chertkov et al. (2008) which represents an efficient truncation scheme on planar graphs and a new representation of the series in terms of Pfaffians of matrices. We analyze in detail both the loop series and the Pfaffian series for models with binary variables and pairwise interactions, and show that the first term of the Pfaffian series can provide very accurate approximations. The algorithm outperforms previous truncation schemes of the loop series and is competitive with other state-of-the-art methods for approximate inference.

Dynamic Policy Programming

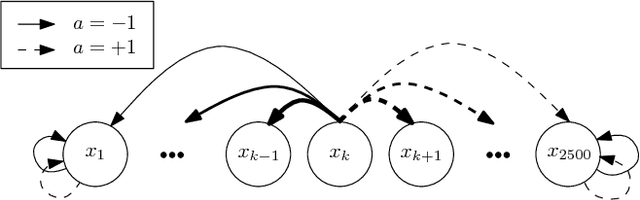
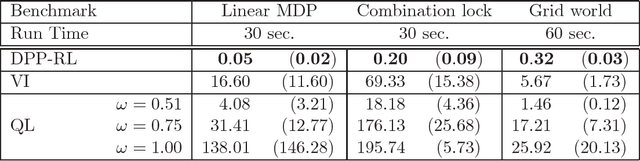
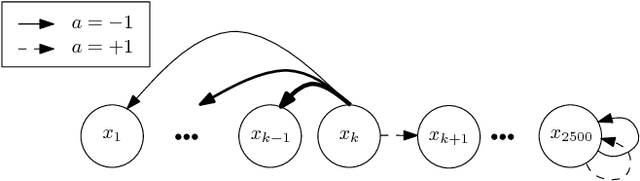
In this paper, we propose a novel policy iteration method, called dynamic policy programming (DPP), to estimate the optimal policy in the infinite-horizon Markov decision processes. We prove the finite-iteration and asymptotic l\infty-norm performance-loss bounds for DPP in the presence of approximation/estimation error. The bounds are expressed in terms of the l\infty-norm of the average accumulated error as opposed to the l\infty-norm of the error in the case of the standard approximate value iteration (AVI) and the approximate policy iteration (API). This suggests that DPP can achieve a better performance than AVI and API since it averages out the simulation noise caused by Monte-Carlo sampling throughout the learning process. We examine this theoretical results numerically by com- paring the performance of the approximate variants of DPP with existing reinforcement learning (RL) methods on different problem domains. Our results show that, in all cases, DPP-based algorithms outperform other RL methods by a wide margin.

Truncating the loop series expansion for Belief Propagation

Recently, M. Chertkov and V.Y. Chernyak derived an exact expression for the partition sum (normalization constant) corresponding to a graphical model, which is an expansion around the Belief Propagation solution. By adding correction terms to the BP free energy, one for each "generalized loop" in the factor graph, the exact partition sum is obtained. However, the usually enormous number of generalized loops generally prohibits summation over all correction terms. In this article we introduce Truncated Loop Series BP (TLSBP), a particular way of truncating the loop series of M. Chertkov and V.Y. Chernyak by considering generalized loops as compositions of simple loops. We analyze the performance of TLSBP in different scenarios, including the Ising model, regular random graphs and on Promedas, a large probabilistic medical diagnostic system. We show that TLSBP often improves upon the accuracy of the BP solution, at the expense of increased computation time. We also show that the performance of TLSBP strongly depends on the degree of interaction between the variables. For weak interactions, truncating the series leads to significant improvements, whereas for strong interactions it can be ineffective, even if a high number of terms is considered.