Local Histogram Matching for Efficient Optical Flow Computation Applied to Velocity Estimation on Pocket Drones

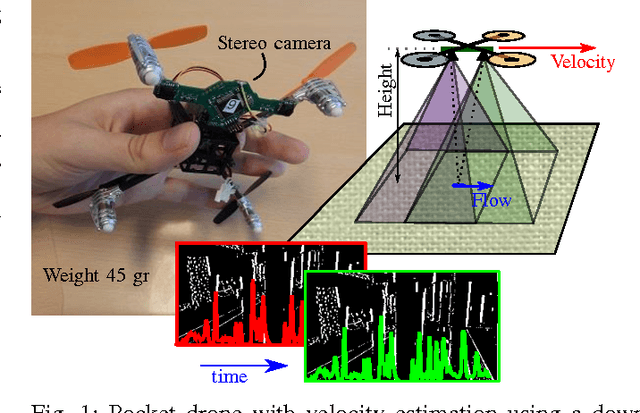
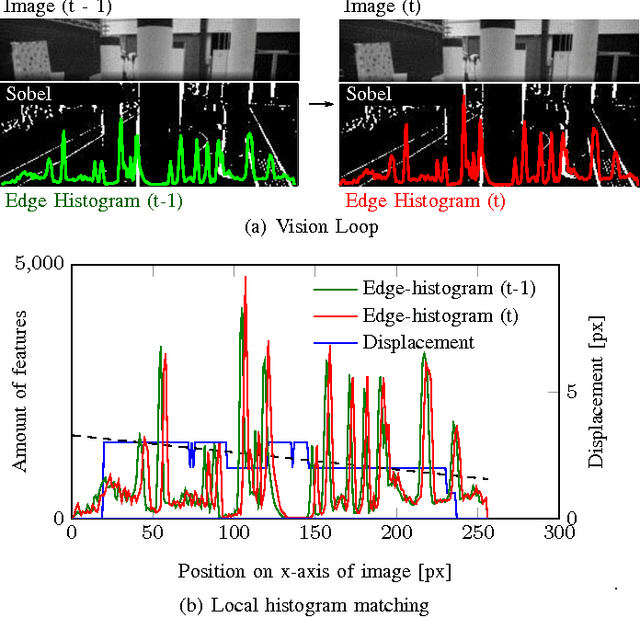
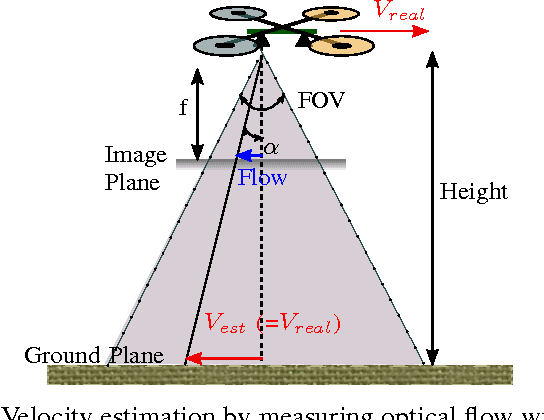
Autonomous flight of pocket drones is challenging due to the severe limitations on on-board energy, sensing, and processing power. However, tiny drones have great potential as their small size allows maneuvering through narrow spaces while their small weight provides significant safety advantages. This paper presents a computationally efficient algorithm for determining optical flow, which can be run on an STM32F4 microprocessor (168 MHz) of a 4 gram stereo-camera. The optical flow algorithm is based on edge histograms. We propose a matching scheme to determine local optical flow. Moreover, the method allows for sub-pixel flow determination based on time horizon adaptation. We demonstrate velocity measurements in flight and use it within a velocity control-loop on a pocket drone.

Efficient Optical flow and Stereo Vision for Velocity Estimation and Obstacle Avoidance on an Autonomous Pocket Drone

Miniature Micro Aerial Vehicles (MAV) are very suitable for flying in indoor environments, but autonomous navigation is challenging due to their strict hardware limitations. This paper presents a highly efficient computer vision algorithm called Edge-FS for the determination of velocity and depth. It runs at 20 Hz on a 4 g stereo camera with an embedded STM32F4 microprocessor (168 MHz, 192 kB) and uses feature histograms to calculate optical flow and stereo disparity. The stereo-based distance estimates are used to scale the optical flow in order to retrieve the drone's velocity. The velocity and depth measurements are used for fully autonomous flight of a 40 g pocket drone only relying on on-board sensors. The method allows the MAV to control its velocity and avoid obstacles.

Approximate inference on planar graphs using Loop Calculus and Belief Propagation

We introduce novel results for approximate inference on planar graphical models using the loop calculus framework. The loop calculus (Chertkov and Chernyak, 2006b) allows to express the exact partition function Z of a graphical model as a finite sum of terms that can be evaluated once the belief propagation (BP) solution is known. In general, full summation over all correction terms is intractable. We develop an algorithm for the approach presented in Chertkov et al. (2008) which represents an efficient truncation scheme on planar graphs and a new representation of the series in terms of Pfaffians of matrices. We analyze in detail both the loop series and the Pfaffian series for models with binary variables and pairwise interactions, and show that the first term of the Pfaffian series can provide very accurate approximations. The algorithm outperforms previous truncation schemes of the loop series and is competitive with other state-of-the-art methods for approximate inference.

Approximate Inference and Constrained Optimization

Loopy and generalized belief propagation are popular algorithms for approximate inference in Markov random fields and Bayesian networks. Fixed points of these algorithms correspond to extrema of the Bethe and Kikuchi free energy. However, belief propagation does not always converge, which explains the need for approaches that explicitly minimize the Kikuchi/Bethe free energy, such as CCCP and UPS. Here we describe a class of algorithms that solves this typically nonconvex constrained minimization of the Kikuchi free energy through a sequence of convex constrained minimizations of upper bounds on the Kikuchi free energy. Intuitively one would expect tighter bounds to lead to faster algorithms, which is indeed convincingly demonstrated in our simulations. Several ideas are applied to obtain tight convex bounds that yield dramatic speed-ups over CCCP.

Sufficient conditions for convergence of Loopy Belief Propagation

We derive novel sufficient conditions for convergence of Loopy Belief Propagation (also known as the Sum-Product algorithm) to a unique fixed point. Our results improve upon previously known conditions. For binary variables with (anti-)ferromagnetic interactions, our conditions seem to be sharp.

Hybrid Variational/Gibbs Collapsed Inference in Topic Models

Variational Bayesian inference and (collapsed) Gibbs sampling are the two important classes of inference algorithms for Bayesian networks. Both have their advantages and disadvantages: collapsed Gibbs sampling is unbiased but is also inefficient for large count values and requires averaging over many samples to reduce variance. On the other hand, variational Bayesian inference is efficient and accurate for large count values but suffers from bias for small counts. We propose a hybrid algorithm that combines the best of both worlds: it samples very small counts and applies variational updates to large counts. This hybridization is shown to significantly improve testset perplexity relative to variational inference at no computational cost.