Hierarchical Average-Reward Linearly-solvable Markov Decision Processes

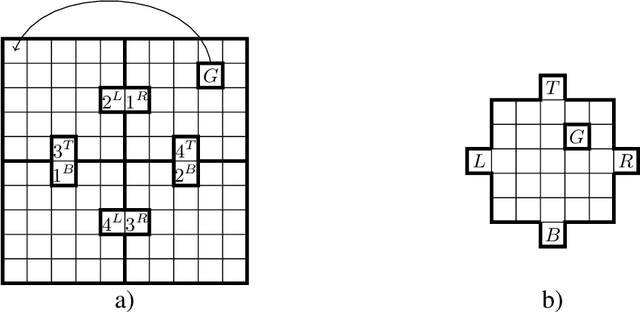
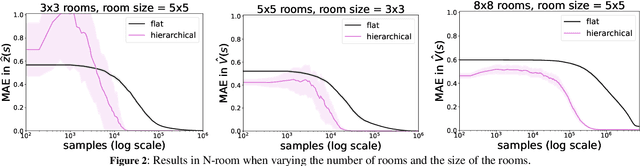
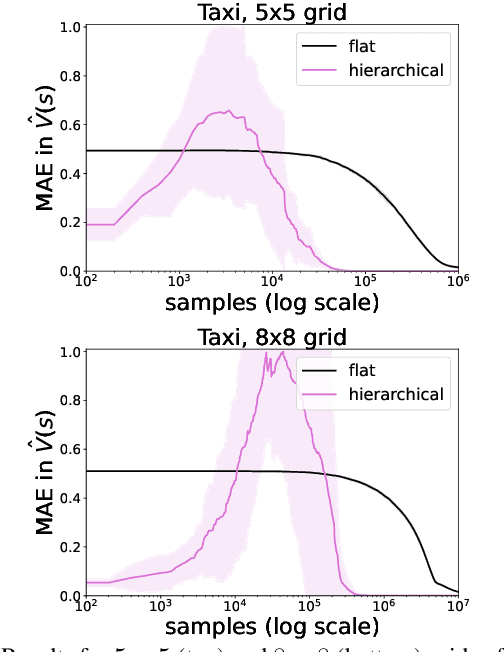
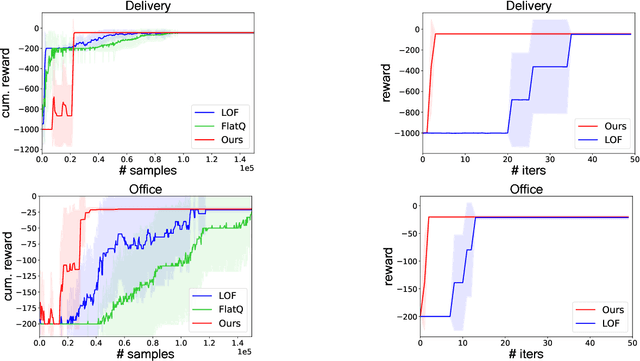
We introduce a novel approach to hierarchical reinforcement learning for Linearly-solvable Markov Decision Processes (LMDPs) in the infinite-horizon average-reward setting. Unlike previous work, our approach allows learning low-level and high-level tasks simultaneously, without imposing limiting restrictions on the low-level tasks. Our method relies on partitions of the state space that create smaller subtasks that are easier to solve, and the equivalence between such partitions to learn more efficiently. We then exploit the compositionality of low-level tasks to exactly represent the value function of the high-level task. Experiments show that our approach can outperform flat average-reward reinforcement learning by one or several orders of magnitude.

Planning with a Learned Policy Basis to Optimally Solve Complex Tasks

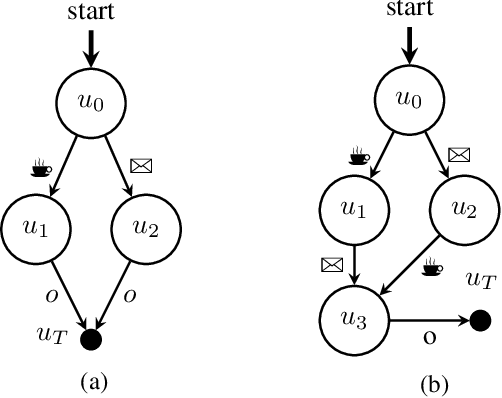
Conventional reinforcement learning (RL) methods can successfully solve a wide range of sequential decision problems. However, learning policies that can generalize predictably across multiple tasks in a setting with non-Markovian reward specifications is a challenging problem. We propose to use successor features to learn a policy basis so that each (sub)policy in it solves a well-defined subproblem. In a task described by a finite state automaton (FSA) that involves the same set of subproblems, the combination of these (sub)policies can then be used to generate an optimal solution without additional learning. In contrast to other methods that combine (sub)policies via planning, our method asymptotically attains global optimality, even in stochastic environments.

Globally Optimal Hierarchical Reinforcement Learning for Linearly-Solvable Markov Decision Processes

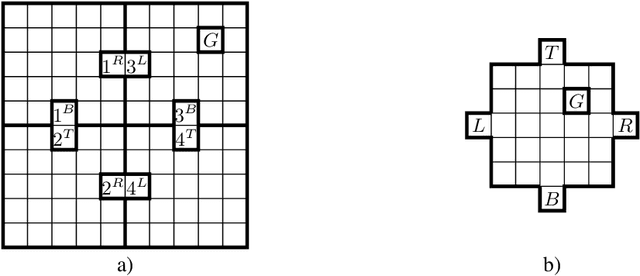
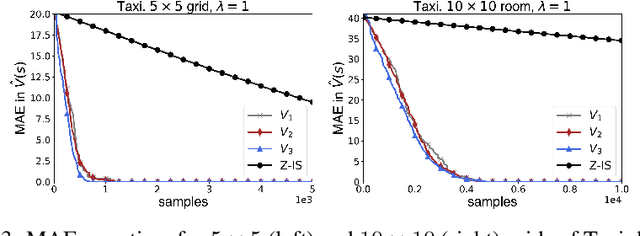
In this work we present a novel approach to hierarchical reinforcement learning for linearly-solvable Markov decision processes. Our approach assumes that the state space is partitioned, and the subtasks consist in moving between the partitions. We represent value functions on several levels of abstraction, and use the compositionality of subtasks to estimate the optimal values of the states in each partition. The policy is implicitly defined on these optimal value estimates, rather than being decomposed among the subtasks. As a consequence, our approach can learn the globally optimal policy, and does not suffer from the non-stationarity of high-level decisions. If several partitions have equivalent dynamics, the subtasks of those partitions can be shared. If the set of boundary states is smaller than the entire state space, our approach can have significantly smaller sample complexity than that of a flat learner, and we validate this empirically in several experiments.