Bisimulation Metrics are Optimal Transport Distances, and Can be Computed Efficiently

We propose a new framework for formulating optimal transport distances between Markov chains. Previously known formulations studied couplings between the entire joint distribution induced by the chains, and derived solutions via a reduction to dynamic programming (DP) in an appropriately defined Markov decision process. This formulation has, however, not led to particularly efficient algorithms so far, since computing the associated DP operators requires fully solving a static optimal transport problem, and these operators need to be applied numerous times during the overall optimization process. In this work, we develop an alternative perspective by considering couplings between a flattened version of the joint distributions that we call discounted occupancy couplings, and show that calculating optimal transport distances in the full space of joint distributions can be equivalently formulated as solving a linear program (LP) in this reduced space. This LP formulation allows us to port several algorithmic ideas from other areas of optimal transport theory. In particular, our formulation makes it possible to introduce an appropriate notion of entropy regularization into the optimization problem, which in turn enables us to directly calculate optimal transport distances via a Sinkhorn-like method we call Sinkhorn Value Iteration (SVI). We show both theoretically and empirically that this method converges quickly to an optimal coupling, essentially at the same computational cost of running vanilla Sinkhorn in each pair of states. Along the way, we point out that our optimal transport distance exactly matches the common notion of bisimulation metrics between Markov chains, and thus our results also apply to computing such metrics, and in fact our algorithm turns out to be significantly more efficient than the best known methods developed so far for this purpose.

Optimisic Information Directed Sampling

We study the problem of online learning in contextual bandit problems where the loss function is assumed to belong to a known parametric function class. We propose a new analytic framework for this setting that bridges the Bayesian theory of information-directed sampling due to Russo and Van Roy (2018) and the worst-case theory of Foster, Kakade, Qian, and Rakhlin (2021) based on the decision-estimation coefficient. Drawing from both lines of work, we propose a algorithmic template called Optimistic Information-Directed Sampling and show that it can achieve instance-dependent regret guarantees similar to the ones achievable by the classic Bayesian IDS method, but with the major advantage of not requiring any Bayesian assumptions. The key technical innovation of our analysis is introducing an optimistic surrogate model for the regret and using it to define a frequentist version of the Information Ratio of Russo and Van Roy (2018), and a less conservative version of the Decision Estimation Coefficient of Foster et al. (2021). Keywords: Contextual bandits, information-directed sampling, decision estimation coefficient, first-order regret bounds.

Lifting the Information Ratio: An Information-Theoretic Analysis of Thompson Sampling for Contextual Bandits

We study the Bayesian regret of the renowned Thompson Sampling algorithm in contextual bandits with binary losses and adversarially-selected contexts. We adapt the information-theoretic perspective of Russo and Van Roy [2016] to the contextual setting by introducing a new concept of information ratio based on the mutual information between the unknown model parameter and the observed loss. This allows us to bound the regret in terms of the entropy of the prior distribution through a remarkably simple proof, and with no structural assumptions on the likelihood or the prior. The extension to priors with infinite entropy only requires a Lipschitz assumption on the log-likelihood. An interesting special case is that of logistic bandits with d-dimensional parameters, K actions, and Lipschitz logits, for which we provide a $\widetilde{O}(\sqrt{dKT})$ regret upper-bound that does not depend on the smallest slope of the sigmoid link function.

Efficient conditioned face animation using frontally-viewed embedding

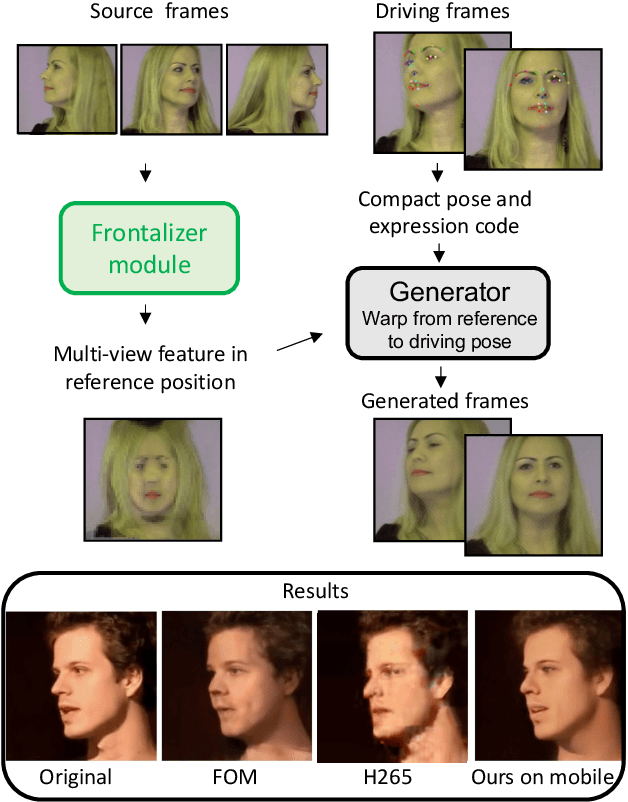
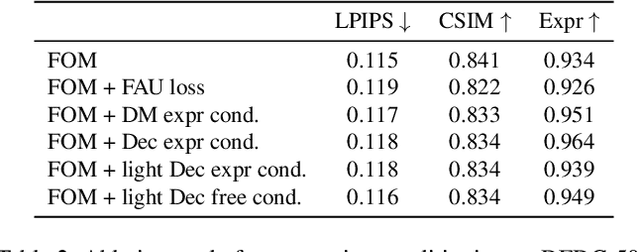
As the quality of few shot facial animation from landmarks increases, new applications become possible, such as ultra low bandwidth video chat compression with a high degree of realism. However, there are some important challenges to tackle in order to improve the experience in real world conditions. In particular, the current approaches fail to represent profile views without distortions, while running in a low compute regime. We focus on this key problem by introducing a multi-frames embedding dubbed Frontalizer to improve profile views rendering. In addition to this core improvement, we explore the learning of a latent code conditioning generations along with landmarks to better convey facial expressions. Our dense models achieves 22% of improvement in perceptual quality and 73% reduction of landmark error over the first order model baseline on a subset of DFDC videos containing head movements. Declined with mobile architectures, our models outperform the previous state-of-the-art (improving perceptual quality by more than 16% and reducing landmark error by more than 47% on two datasets) while running on real time on iPhone 8 with very low bandwidth requirements.